冲刺Noip2017模拟赛7 解题报告—

1、二叉树（binary）

．二叉树
(binary.cpp/c/pas)
【问题描述】
二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（）左、右子树也分别为二叉排序树；
（）没有键值相等的结点。
完全二叉树：只有最下面的两层结点度能够小于2，并且最下面一层的结点
都集中在该层最左边的若干位置的二叉树。
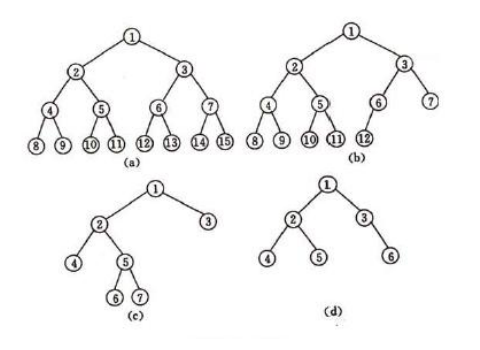
图1中，(a)和(b)是完全二叉树，(c)和(d)是非完全二叉树。
给出N个数，且这N个数构成1至N的排列。现在需要你按顺序构建一棵二叉
排序树，并按照层次遍历的方式输出它，然后判断它是否是一棵完全二叉树。
【输入格式】
输入文件名为binary.in。
输入文件包含两行。第一行为一个正整数N；第二行为1至N的排列。
【输出格式】
输出文件名为binary.out。
输出文件包含两行。第一行为构建出的二叉排序树的层次遍历；第二行判
断是否是完全二叉树：若是输出yes，否则输出no。
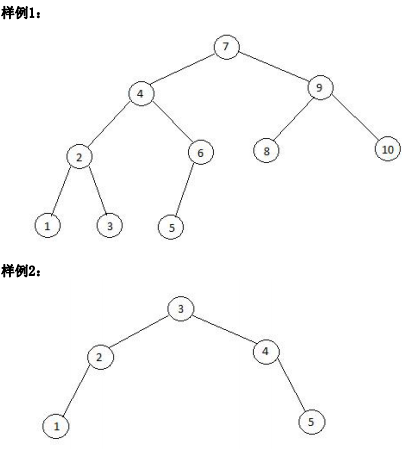
【输入输出样例1】
binary.in
 
binary.out
 
yes
【输入输出样例2】
binary.in 
 
binary.out
 
no
【数据规模与约定】
对于100%的数据，≤N≤。

题目

tag：模拟

思路：其实这道题没有看上去那么复杂。插入的时候比节点大就往右走，反之往左走，走到头了放进去，最后建个树。判断是不是完全二叉树要看最大的节点是不是在自己应该在的位置，因为仔细观察发现完全二叉树是每一层从左往右一个一个放，每个节点的数值和编号应该相等（感谢dalao这句话的思路）。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 using namespace std;
 int maxx,list[][],tree[<<],deep,n;
 void insert(int o,int x)
 {
     maxx=max(maxx,o);
     if(!tree[o]){
         tree[o]=x;
         return;
     }
     if(x>tree[o]) insert(o<<|,x);
     else insert(o<<,x);
 }
 void dfs(int o,int f)
 {
     deep=max(deep,f);
     if(tree[o<<]){
         list[f+][++list[f+][]]=tree[o<<];
         dfs(o<<,f+);
     }
     if(tree[o<<|]){
         list[f+][++list[f+][]]=tree[o<<|];
         dfs(o<<|,f+);
     }
 }
 int main()
 {
     //freopen("binary.in","r",stdin);
     //freopen("binary.out","w",stdout);
     int x;
     scanf("%d",&n);
     for(int i=;i<=n;++i){
         scanf("%d",&x);
         insert(,x);
     }
     list[][]=tree[];
     list[][]=;
     dfs(,);
     for(int i=;i<=deep;++i)
         for(int j=;j<=list[i][];++j)
             printf("%d ",list[i][j]);
     puts("");
     if(maxx!=n) puts("no");
     else puts("yes");
     return ;
 }

2、列车调度(manage)

【问题描述】
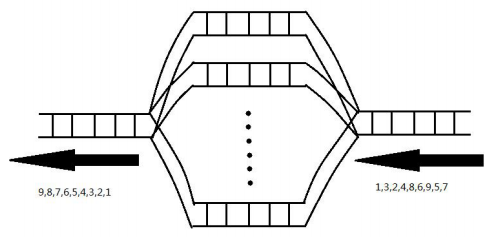
有N辆列车，标记为1,,,…,N。它们按照一定的次序进站，站台共有K个轨
道，轨道遵从先进先出的原则。列车进入站台内的轨道后可以等待任意时间后出
站，且所有列车不可后退。现在要使出站的顺序变为N,N-,N-,…,，询问K的
最小值是多少。
例如上图中进站的顺序为1,,,,,,,,，则出站的顺序变为
,,,,,,,,。
【输入格式】
输入文件名为manage.in。
输入共2行。
第  行包含1个正整数N，表示N辆列车。
第  行包含N个正整数，为1至N的一个排列，表示进站次序。
【输出格式】
输出文件名为manage.out。
输出共1行，包含1个整数，表示站台内轨道数K的最小值。
【输入输出样例1】
manage.in
 
manage.out
 
【输入输出样例2】
manage.in
 
manage.out
 
【数据规模与约定】
对于 %的数据，N≤；
对于 %的数据，N≤；
对于 %的数据，N≤。

题目

tag：二分查找

思路：单纯模拟用时较长（但是O（n2）居然能过？？？），正解是构造非降序列，比如现在的序列是（5,6,9,11），要把10插入进去，5,6,9都比10小，11比10大就停在11后面，序列变成（5,6,9,10），虽然单个的数值改变了，但是原本的单调性没变，因此我们可以二分查找第一个比要插入的数大的数（0011型）。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cstdlib>
 #define maxn 100010
 using namespace std;
 int n,a[maxn],f[maxn],ans=;
 int main()
 {
     //freopen("manage.in","r",stdin);
     //freopen("manage.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i) scanf("%d",&a[i]);
     f[]=a[];
     for(int i=;i<=n;++i){
         int l=lower_bound(f+,f+ans+,a[i])-f;
         f[l]=a[i];
         ans=max(ans,l);
     }
     printf("%d",ans);
     return ;
 }

3、保留道路（road）

【问题描述】
很久很久以前有一个国家，这个国家有N个城市，城市由1,,,…,N标号，
城市间有M条双向道路，每条道路都有两个属性g和s，两个城市间可能有多条道
路，并且可能存在将某一城市与其自身连接起来的道路。后来由于战争的原因，
国王不得不下令减小花费从而关闭一些道路，但是必须要保证任意两个城市相互
可达。
道路花费的计算公式为wG*max{所有剩下道路的属性g}+wS*max{所有剩下道
路的属性s}，其中wG和wS是给定的值。国王想要在满足连通性的前提下使这个花
费最小，现在需要你计算出这个花费。
【输入格式】
输入文件名为road.in。
第一行包含两个正整数N和M。
第二行包含两个正整数wG和wS。
后面的M行每行描述一条道路，包含四个正整数u,v,g,s，分别表示道路连接
的两个城市以及道路的两个属性。
【输出格式】
输出文件名为road.out。
输出一个整数，表示最小花费。若无论如何不能满足连通性，输出-。
【输入输出样例】
road.in
 
road.out
 
【数据规模与约定】
对于 %的数据，N≤，M≤；
对于 %的数据，N≤，M≤；
对于 %的数据，N≤，M≤；
对于 %的数据，N≤，M≤，wG,wS,g,s≤。

题目

tag：最小生成树、轻度玄学（雾）

思路：二维费用的kruskal，很有研究的价值。平时我们做的最小生成树都只有一维，突然多了一个维度，而且还有系数，有点让人手足无措，我们应当以什么标准来选择，加和？乘积？比值？都不行吧，可以随便举反例。正解是，两个权值g,s任选其一作为标准从小到大排序，比如选择g就以g的大小排，再看s的大小，我们造一个栈，从底到顶s从小到大，每放一条边调整栈中各边的位置，做一遍kruskal，记录答案，时间复杂度是O(nm)。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #define maxn 100010
 #define ll long long
 #define inf 1ll<<60
 using namespace std;
 int gmax,smax,n,m,G,S,fa[maxn],st[maxn],top,tot;
 ll ans=inf;
 struct Edge{
     int u,v,g,s;
 }e[maxn];
 bool cmp(Edge x,Edge y)
 {
     return x.g<y.g;
 }
 int find(int x)
 {
     return x==fa[x]?x:fa[x]=find(fa[x]);
 }
 int main()
 {
     //freopen("road.in","r",stdin);
     //freopen("road.out","w",stdout);
     int u,v,g,s;
     scanf("%d%d",&n,&m);
     scanf("%d%d",&G,&S);
     for(int i=;i<=m;++i) scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].g,&e[i].s);
     sort(e+,e+m+,cmp);
     for(int i=;i<=m;++i){
         int j=;
         for(j=;j<=n;++j) fa[j]=j;
         for(j=top;j>=;--j)
             if(e[st[j]].s>e[i].s)
                 st[j+]=st[j];
             else break;
         top++;
         st[j+]=i;
         tot=;
         for(j=;j<=top;++j)
         {
             int k1=find(e[st[j]].u),k2=find(e[st[j]].v);
             if(k1!=k2){
                 fa[k1]=k2;
                 st[++tot]=st[j];
             }
             if(tot==n-) break;
         }
         if(tot==n-) ans=min(ans,1ll*e[i].g*G+1ll*e[st[n-]].s*S);
         top=tot;
     }
     if(ans==inf) printf("-1");
     else printf("%I64d",ans);
     return ;
 }

————————————————懒得打分割线啊——————————————————

芒果君：考了这么多次，这场翻车最厉害，都倒数了QAQ 还是想太多