【编程开发】非对称加密过程详解(基于RSA非对称加密算法实现)
到这里,公钥和密钥已经确定。公钥为(N, e) = (33, 3),密钥为(N, d) = (33, 7)。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public class SimpleRSA /** * * * * */ public static long rsa(int baseNum, int key, long message){ if(baseNum1 ||1){ return 0L; } //加密或者解密之后的数据 long rsaMessage //加密核心算法 rsaMessage return rsaMessage; } public static void main(String[] //基数 int baseNum3 * 11; //公钥 int keyE3; //密钥 int keyD7; //未加密的数据 long msg //加密后的数据 long encodeMsg //解密后的数据 long decodeMsg System.out.println("加密前:" + System.out.println("加密后:" + System.out.println("解密后:" + }} |
B. Alice 对数字信息进行哈希(hash)运算,得到一个信息摘要。
F. Bob 用Alice 的公钥(PK)对Alice 的数字签名进行解密,得到信息摘要。
【编程开发】非对称加密过程详解(基于RSA非对称加密算法实现)的更多相关文章
- 【转载】非对称加密过程详解(基于RSA非对称加密算法实现)
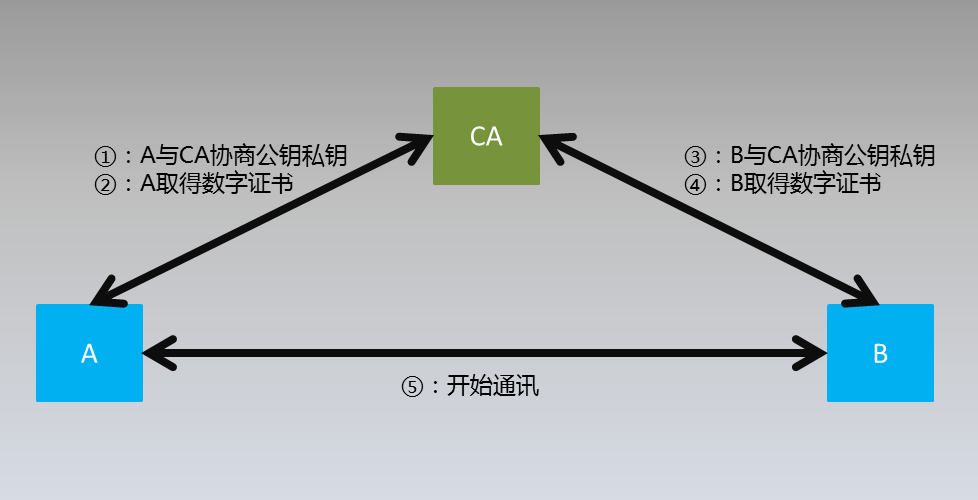
1.非对称加密过程: 假如现实世界中存在A和B进行通讯,为了实现在非安全的通讯通道上实现信息的保密性.完整性.可用性(即信息安全的三个性质),A和B约定使用非对称加密通道进行通讯,具体 ...
- MapReduce过程详解(基于hadoop2.x架构)
本文基于hadoop2.x架构详细描述了mapreduce的执行过程,包括partition,combiner,shuffle等组件以及yarn平台与mapreduce编程模型的关系. mapredu ...
- C++编程规范和编译过程详解
前言:因为c++基础打得不牢,所以准备花点时间再学一下c++的基础知识,主要是看网易云课堂里面的免费课程,把一些知识点做个笔记记下来. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ...
- Swift 对象创建(PUT Object)过程详解——基于副本策略(一)
swift中创建对象,即PUT object,根据选定的存储策略将对象内容写入至相应的服务器(object server).我们重点关注object controller和object servers ...
- nrf52——DFU升级USB/UART升级方式详解(基于SDK开发例程)
摘要:在前面的nrf52--DFU升级OTA升级方式详解(基于SDK开发例程)一文中我测试了基于蓝牙的OTA,本文将开始基于UART和USB(USB_CDC_)进行升级测试. 整体升级流程: 整个过程 ...
- 个人用户永久免费,可自动升级版Excel插件,使用VSTO开发,Excel催化剂安装过程详解及安装失败解决方法
因Excel催化剂用了VSTO的开发技术,并且为了最好的用户体验,用了Clickonce的布署方式(无需人工干预自动更新,让用户使用如浏览器访问网站一般,永远是最新的内容和功能).对安装过程有一定的难 ...
- SSL/TLS 握手过程详解
在现代社会,互联网已经渗透到人们日常生活的方方面面,娱乐.经济.社会关系等都离不开互联网的帮助.在这个背景下,互联网安全就显得十分重要,没有提供足够的安全保障,人们是不会如此依赖它的.幸运的是,在大牛 ...
- (转)Linux 开机引导和启动过程详解
Linux 开机引导和启动过程详解 编译自:https://opensource.com/article/17/2/linux-boot-and-startup作者: David Both 原创:LC ...
- 开源项目SMSS发开指南(五)——SSL/TLS加密通信详解(下)
继上一篇介绍如何在多种语言之间使用SSL加密通信,今天我们关注Java端的证书创建以及支持SSL的NioSocket服务端开发.完整源码 一.创建keystore文件 网上大多数是通过jdk命令创建秘 ...
随机推荐
- P4295 [SCOI2003]严格N元树 DP
思路:DP 提交:\(5\)次 错因:2次高精写错(我太菜了),2次写错特判 题解: 设\(f[i]\)表示深度\(\leq i\)的严格\(n\)元树的数目,有 \[f[i]=pow(f[i-1], ...
- codeforces 1249 D2 Too Many Segments (hard version) 贪心+树状数组
题意 给定n个线段,线段可以相交,第\(i\)个线段覆盖的区间为\([l_i,r_i]\),问最少删除多少个线段让覆盖每个点的线段数量小于等于k. 分析 从左往右扫每个点\(x\),若覆盖点\(x\) ...
- python编写弹球游戏的实现代码
#coding:utf- from tkinter import * import random import time class Ball: #创建一个球类 def __init__(self, ...
- 常用exporter下载
1.node_exporter https://github.com/prometheus/node_exporter/releases/download/v0.18.1/node_exporter- ...
- Spring Cloud Config(二):基于Git搭建配置中心
1.简述 本文选用Git作为配置仓库,新建两个环境的配置文件夹,dev 和 test,文件夹中分别存放 Config Client 端的配置文件,目录结构如下: ├ ─ ─ dev └ ─ ─ con ...
- deepin安装下载,部署在虚拟机上
第一次接触linux就用了很久的Ubuntu,后来尝试了Manjaro.Debian,还是用了Ubuntu,但是用VM虚拟机使用的ubuntu经常卡顿.我始终觉得ubuntu的默认桌面环境gnome可 ...
- zabbix监控windows案例
首先在zabbix官网下载zabbix软件包:https://www.zabbix.com/ 下载完成之后,将其解压到D盘 # 配置与安装,配置zabbix agent相关配置. 找到conf下的配置 ...
- MySQL的概述和基础(学习整理)
1. 数据库基本概念 数据库(DataBase,DB)是用来存储和管理数据的仓库.与其他种类存储和管理数据的方式有所不同的是,数据库是兼持久化存储数据.便捷存储管理数据.使用统一的方式操作数据库几个特 ...
- EntityFramework Core Code First 已有数据库
问题场景:我已经有一个数据库,想用 EF core Code First,怎么办? 首先,可以参考微软的API文档:通过现有数据库在 ASP.NET Core 上开始使用 EF Core, 这一步可以 ...
- intellj idea 常用快捷键
1.command+shift+a 查找操作2.command+e 查找历史打开的文件3.command+n 查找类4.command+shift+n 查找文件
