Python3多重继承排序原理（C3算法）

　　参考：https://www.jianshu.com/p/c9a0b055947b

　　　　　https://xubiubiu.com/2019/06/10/python-%E6%96%B9%E6%B3%95%E8%A7%A3%E6%9E%90%E9%A1%BA%E5%BA%8Fmro-c3%E7%AE%97%E6%B3%95/

　　

　　类C的线性化记忆为L[C]=[C1,C2,...Cn]，其中C1称为L[C]的头，其余元素[C2,...Cn]称为尾。如果一个类C继承自基类B1,B2,...，B那么L[C]的计算过程为

　　

#类object为最高父类，所有类都继承object
L[objicet]=[object]
L[C(B1,B2,...Bn)]=[C]+merge(L[B1],L[B2],[B1,B2,...Bn])

　　merge是将一组列表输出为一个列表，其过程为

1，检查第一个列表的头元素，记做H
2，如果H是后续序列的第一个元素，或者不在后续序列中再次出现，则将其输出，并将其从所有列表中删除，如果不符合跳过此元素，查找下一个列表的第一个元素，然后回到步骤1
3，重复上述步骤，直至列表为空或者不能再找出可以输出的元素。

　　举例说明

>>> class A(object):
...  pass
...
>>> class B(object):
...  pass
...
>>> class C(A,B):
...   pass

　

　　首先object,A,B的线性化结果比较简单

L[object]=[object]
L[A]=[A,object]
L[B]=[B,object]

　　python内置变量__mro__存储了

>>> object.__mro__
(<class 'object'>,)
>>> A.__mro__
(<class '__main__.A'>, <class 'object'>)
>>> B.__mro__
(<class '__main__.B'>, <class 'object'>)

　　需要计算出L[C]

L[C]=[C]+merge(L[A],L[B],[A,B])
    =[C]+mergr([A,object],[B,object],[A,B])
	#取得的第一个元素是A，是序列[A,B]的第一个元素所以输出A并且将A从所有列表中删除
	=[C,A]+merge([object],[B,object],[B])
	#取得的元素为object不满足条件，object是序列[B,object]的最后一个元素，跳过取到元素为B，满足条件，将B输出并从所有列表删除B
	=[C,A,B]+merge([object],[object])
	#最后的结果
	=[C,A,B,object]

　　使用__mro__验证计算结果正确

>>> C.__mro__
(<class '__main__.C'>, <class '__main__.A'>, <class '__main__.B'>, <class 'object'>)

　　一个复杂的例子

class B(object): pass

class C(object): pass

class D(A,C): pass

class E(B,C): pass

class F(D,E): pass

　　计算过程

L[F] = [F] + merge(L[D], L[E], [D, E])
     = [F] + merge([D, A, C, object], [E, B, C, object],  [D, E])
     = [F, D] + merge([A, C, object], [E, B, C, object],  [E])
     = [F, D, A] + merge([C, object], [E, B, C, object], [E])
     = [F, D, A, E] + merge([C, object], [B, C, object])
     = [F, D, A, E, B] + merge([C, object], [C, object])
     = [F, D, A, E, B, C, object]

　　验证计算结果

(<class '__main__.F'>, <class '__main__.D'>, <class '__main__.A'>, <class '__main__.E'>, <class '__main__.B'>, <class '__main__.C'>, <class 'object'>)

　　

　　以上算法虽然可以计算出继承顺序，但是不直观 ，可以使用图示拓扑顺序进行推导

　　什么是拓扑顺序

　　在图论中，拓扑顺序(Topological Storting)是一个有向无环图（DAG,Directed Acyclic Graph）的所有定点的线性序列。且该序列必须满足一下两个条件

　　1，每个顶点出现且只出现一次

2，若存在一条从顶点A到顶点B的路径，那么在序列中顶点A出现在顶点B的前面

　　看下图

　　它是一个DAG图，那么如果写出它的拓扑顺序呢？一种比较常见的方法

　　1，从DAG途中选择一个没有前驱（即入度为0）的顶点并输出

2，从图中删除该顶点和所有以它为起点的有向边

3，重复1和2直到当前DAG图为空或者当前途中不存在无前驱的顶点为止。

　　于是得到拓扑排序后的结果为{1,2,4,3,5}

　　看实例

class A(object):
  pass

class B(object):
  pass

class C1(A,B):
  pass

class C2(A,B):
  pass

class D(C1,C2):
  pass

　　根据上述继承关系构成一张图

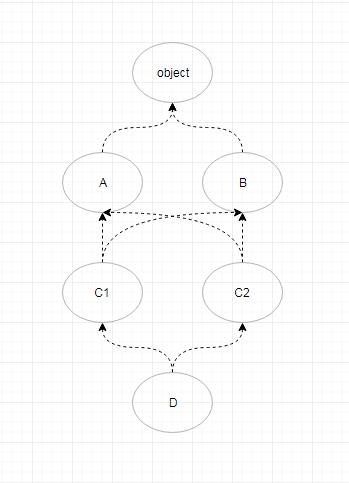
　　1，找到入度为0的点，只有一个D，把D拿出来，把D相关的边减掉

　　 2，现在有两个入度为0的点(C1,C2),取最左原则，拿C1，减掉C1相关的边，这时候的排序是{D,C1}

3, 现在入度为0的点(C2),拿掉C2，减掉C2相关的边，这时候的排序是{D,C1,C2}

　　4,现在入度为0的点(A,B),取最左原则，拿掉A，减掉A相关的边，这时候的排序是{D,C1,C2,A}

5,现在入度为0的点只有B，拿掉B，减掉B相关的边，最后只剩下object

所以最后的排序是{D,C1,C2,A,B,object}

验证一下结果

>>> D.__mro__
(<class '__main__.D'>, <class '__main__.C1'>, <class '__main__.C2'>, <class '__main__.A'>, <class '__main__.B'>, <class 'object'>)

　　

　　为了进一步属性，在看一个例子

class A(object):
  pass

class B(object):
  pass

class C1(A):
  pass

class C2(B):
  pass

class D(C1,C2):
  pass

　　继承图

　　1，找到入度为0的顶点，只有一个D，拿D，剪掉D相关的边

　　2，得到两个入度为0的顶点(C1,C2),根据最左原则，拿C1，剪掉C1相关的边，这时候序列为{D,C1}

　　3，接着看，入度为0的顶点有两个(A,C1),根据最左原则，拿A，剪掉A相关的边，这时候序列为{D,C1,A}

　　4，接着看，入度为0的顶点为C2,拿C2，剪掉C2相关的边，这时候序列为{D,C1,A,C2}

　　5，继续，入度为0的顶点为B，拿B，剪掉B相关的边，最后还有一个object

　　所以最后的序列为{D,C1,A,C2,B,object}

(<class '__main__.D'>, <class '__main__.C1'>, <class '__main__.A'>, <class '__main__.C2'>, <class '__main__.B'>, <class 'object'>)

　　使用图示拓扑法可以快速计算出继承顺序