数据库索引 B+树

问题1.数据库为什么要设计索引？
索引类似书本目录，用于提升数据库查找速度。
问题2.哈希（hash）比树（tree）更快，索引结构为什么要设计成树型？
加快查找速度的数据结构，常见的有两类：
（1）哈希，例如HashMap，查询/插入/修改/删除的平均时间复杂度都是O(1)；
（2）树，例如平衡二叉搜索树，查询/插入/修改/删除的平均时间复杂度都是O(lg(n))；
可以看到，不管是读，还是写，哈希类型的索引都比树型的索引更快一些，那为什么，索引结构要设计成树型呢？
索引设计成树型，和SQL的需求有关。
对于一个单行查询SQL需求：
select * from t where name = "mysql";
确实是哈希表索引更快，因为每次都是只查询一条记录。
索引如果业务需求都是单行访问，确实可以使用哈希索引。
但是对于排序查询的SQL需求：
分组group by、排序order by、比较< >、不等于...
哈希型的索引，事件复杂度会退化为O(n)，而树型的“有序特性”，依然能够保持O(log(n))的高效率。
Mysql为了实现SQL多种多样需求故而默认用树实现索引。
但InnoDB并不支持哈希索引。
问题3.数据库索引为什么使用B+树？
下面先来介绍几种树。
第一种：二叉搜索树

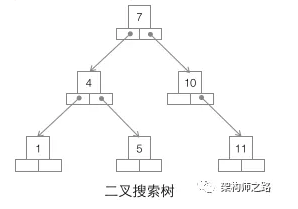
二叉搜索树是最为大家熟知的一种数据结构，它为什么不适合用作数据库索引？
（1）当数据量大的时候，树的高度会比较高，数据量大的时候，查询会比较慢；
（2）每个节点只存储一个记录，可能导致一次查询有很多次磁盘IO；
第二种树：B树

B树的特点是：
（1）不再是二叉搜索，而是m叉搜索；
（2）叶子节点，非叶子节点，都存储数据；
（3）中序遍历，可以获得所用节点；
（4）非根节点包含的关键字个数j满足，（m/2）-1 <=j<= m-1，节点分裂时要满足这个条件。
B树被作为实现索引的数据结构被创造出来，是因为它能够完美的利用“局部性原理”。
什么是局部性原理？
局部性原理的逻辑是这样的：
（1）内存读写快，磁盘读写慢，而且慢很多；
（2）磁盘预读：磁盘读写并不是按需读取，而是按页读取，一次会读取一页的数据，每次加载更多的数据，如果未来要读取的数据就在这一页中，可以避免未来的磁盘IO，提高效率。通常一页数据是4K；
（3）局部性原理：软件设计要尽量遵循“数据读取集中”与“使用到一个数据，大概率会使用其附近的数据”，这样磁盘预读能充分提高磁盘IO；
B树为何适合做索引？
（1）由于是m分叉的，高度能够大大降低；
（2）每个节点可以存储j个记录，如果将节点大小设置为页大小，例如4K，能够充分的利用预读的特性，极大减少磁盘IO；
第三种树：B+树

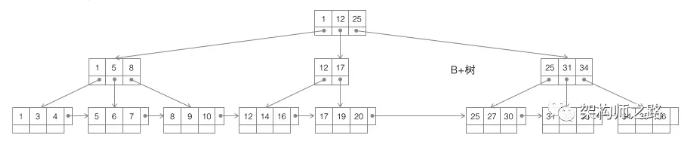
B+树，仍是m叉搜索树，在B树的基础上，做了一些改进：
（1）非叶子节点不再存储数据，数据只存储在同一层的叶子节点上（B+树中根到每一个节点的路径长度一样，而B树不是这样）；
（2）叶子之间，增加了链表，获取所有节点，不再需要中序遍历；
这些改进让B+树比B树有更优的特性：
（1）范围查找，定位min与max之后，中间叶子节点就是结果集，不用中序回溯。范围查询在SQL中用的很多，这是B+树比B树最大的优势；
（2）叶子节点存储实际记录行，记录行相对比较紧密的存储，适合大数据量磁盘存储；非叶子节点存储记录的PK，用于查询加速，适合内存存储；
（3）非叶子节点，不存储实际记录，而只存储记录的KEY的话，那么在相同内存下，B+树能够存储更多索引；
最后量化说下，为什么m叉的B+树比二叉搜索树的高度大大大大降低？
（1）局部性原理，将一个节点的大小设置为一页，一页4K，假设一个KEY有8字节，一个节点可以存储500个KEY，即j=500
（2）m叉树，大概m/2<=j<=m，即可以差不多是1000叉树
（3）那么：
一层树：1个节点，1*500个KEY，大小4K
二层树：1000个节点，1000*500=50W个KEY，大小1000*4K=4M
三层树：1000*1000个节点，1000*1000*500=5亿个KEY，大小1000*1000*4K=4G
可以看到，存储大量的数据（5亿），并不需要太高树的深度（高度3），索引也不是太占内存（4G）。

总结
数据库索引用于加快查询速度
虽然哈希索引是O(1)，树索引是O(log(n))，但SQL有很多有序需求，古数据库使用树型索引
InnoDB不支持哈希索引
数据预读的思路是：磁盘读写并不是按需读取，而是按页预读，一次会读一页的数据，每次加载更多的数据，以便未来减少磁盘IO
局部性原理：软件设计要尽量遵循“数据读取集中”与“使用到一个数据，大概率会使用其附近的数据”，这样磁盘预读能充分提高磁盘IO
数据库的索引常用B+树：
（1）很适合磁盘存储，能够充分利用局部性原理，磁盘预读；
（2）很低的树高度，能够存储大量数据；
（3）索引本身占用的内存很小；
（4）能够很好的支持单点查询，范围查询，有序性查询。
本文学习自公众号“架构师之路”，感谢作者的奉献