dfs 序 欧拉序

推荐博客 ：https://www.cnblogs.com/stxy-ferryman/p/7741970.html

　　DFS序其实就是一棵树顺次访问的结点的顺序，例如下面这棵树

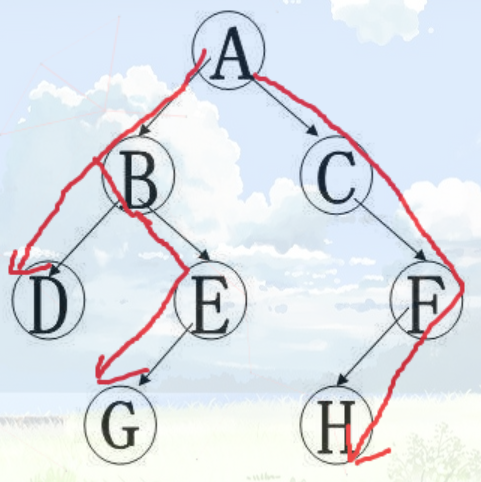
它的 dfs 序就是 A-B-D-E-G-C-F-H

int key = 0;
void dfs(int x, int fa){
    dfs_[cnt++] = x;
    s[x] = ++key;
    for(int i = 0 ; i < ve[x].size(); i++){
        int to = ve[x][i];
        if (to == fa) continue;
        dfs(to, x);
    }
    //dfs_[cnt++] = x;
    e[x] = key;
}

我们这里的 dfs_[ ] 数组表示的就是这棵树的 dfs 序，s[ ] 与 e[ ] 数组表示的就是访问某个结点的时间顺序。

借助 dfs序，我们可以将树的结点变成一维的数组的形式，观察上面的图，B的子树中的结点有DEG,其在 dfs序中也是连续的。因此可以通过时间戳很容易找到子树的开始时间和结束时间。

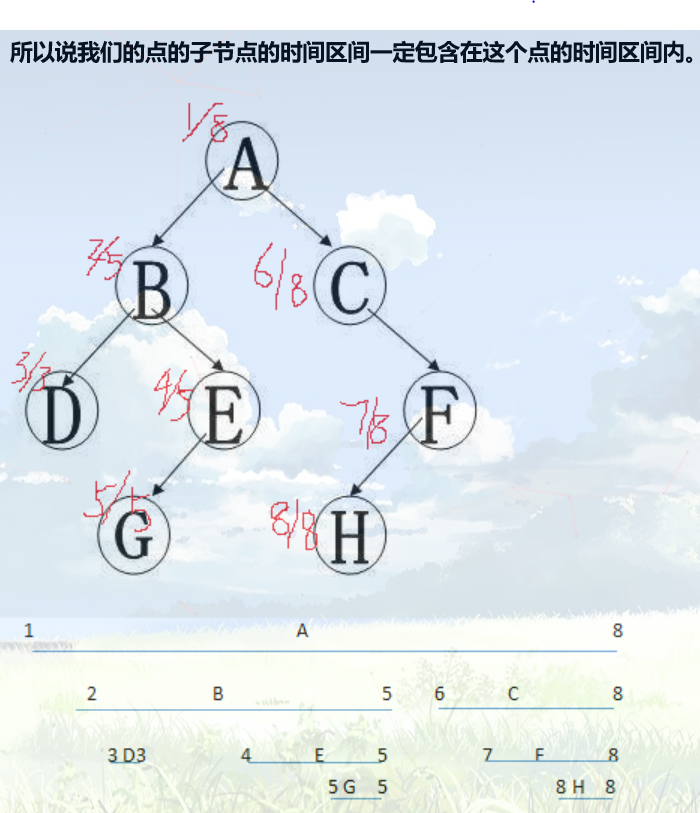
可以发现作为子树的时间戳一定在其内部。

通过这个dfs序我们还可以做很多事情，比如给你一颗 n 个结点的树，m 个操作，每次操作可以使某一棵子树全部加上或减去某一个值，问最后每个点的值是多少， 或某个子树的权值之和是多少？

看到这里再想这个问题就很简单了，找到dfs序，利用差分，就可以实现 o(1)的修改了。

二 、 欧拉序

欧拉序，就是从根节点出发，按照dfs顺序在绕回到根节点，其有两种不同的写法

（ 1 ）

int cnt = 1;
void dfs(int x, int fa){
    dfs_[cnt++] = x;
    for(int i = 0 ; i < ve[x].size(); i++){
        int to = ve[x][i];
        if (to == fa) continue;
        dfs(to, x);
        dfs_[cnt++] = x;
    }
}

(2)

int cnt = 1;
void dfs(int x, int fa){
    dfs_[cnt++] = x;
    for(int i = 0 ; i < ve[x].size(); i++){
        int to = ve[x][i];
        if (to == fa) continue;
        dfs(to, x);
    }
    dfs_[cnt++] = x;
}

这两种是比较常见的欧拉序的写法。

那么欧拉序有什么用呢？

　　还是上面提到的问题，我们会发现所有的字母都出现了两次，相同的两个字母之间表示以其为根的所有子树，注意这些点都是出现两次的。计算的时候同样是将差分的数组累加，最后除以2即可。