用数学解赌博问题不稀奇，用赌博解数学问题才牛B

有一个经典的概率问题：平均需要抛掷多少次硬币，才会首次出现连续的 n 个正面？它的答案是 2^(n+1) – 2 。取 n=2 的话，我们就有这样的结论：平均要抛掷 6 次硬币，才能得到两个连续的正面。或许这个期望次数比你想象中的要多吧。我们不妨试着来验证一下这一结果。由简单的递推可得，所有 1 都不相邻的 k 位 01 串有 Fk+2 个，其中 Fi 表示 Fibonacci 数列中的第 i 项。而“抛掷第 k 次才出现连续两个正面”的意思就是， k 位 01 串的末三位是 011 ，并且前面 k – 3 位中的数字 1 都不相邻。因此，在所有 2^k 个 k 位 01 串中，只有 Fk-1 个是满足要求的。因此，我们要求的期望值就等于 ∑ (k=2..∞) k * Fk-1 / 2^k 。这个无穷级数就等于 6 。我怎么算的呢？我用 Mathematica 算的。

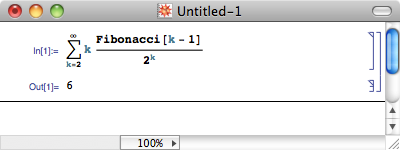
显然，当 n 更大的时候，期望值的计算更加复杂。而简单美妙的结论让我们不由得开始思考，这个问题有没有什么可以避免计算的巧妙思路？万万没有想到的是，在赌博问题的研究中，概率论帮了不少大忙；而这一回，该轮到赌博问题反过来立功了。

设想有这么一家赌场，赌场里只有一个游戏：猜正反。游戏规则很简单，玩家下注 x 元钱，赌正面或者反面；然后庄家抛出硬币，如果玩家猜错了他就会输掉这 x 元，如果玩家猜对了他将得到 2x 元的回报（也就是净赚 x 元）。
    让我们假设每一回合开始之前，都会有一个新的玩家加入游戏，与仍然在场的玩家们一同赌博。每个玩家最初都只有 1 元钱，并且他们的策略也都是相同的：每回都把当前身上的所有钱都押在正面上。运气好的话，从加入游戏开始，庄家抛掷出来的硬币一直是正面，这个玩家就会一直赢钱；如果连续 n 次硬币都是正面朝上，他将会赢得 2^n 元钱。这个 2^n 就是赌场老板的心理承受极限——一旦有人赢到了 2^n 元钱，赌场老板便会下令停止游戏，关闭赌场。让我们来看看，在这场游戏中存在哪些有趣的结论。

首先，连续 n 次正面朝上的概率虽然很小，但确实是有可能发生的，因此总有一个时候赌场将被关闭。赌场关闭之时，唯一赚到钱的人就是赌场关闭前最后进来的那 n 个人。每个人都只花费了 1 元钱，但他们却赢得了不同数量的钱。其中，最后进来的人赢回了 2 元，倒数第二进来的人赢回了 4 元，倒数第 n 进来的人则赢得了 2^n 元（他就是赌场关闭的原因），他们一共赚取了 2 + 4 + 8 + … + 2^n = 2^(n+1) – 2 元。其余所有人初始时的 1 元钱都打了水漂，因为没有人挺过了倒数第 n + 1 轮游戏。
    另外，由于这个游戏是一个完全公平的游戏，因此赌场的盈亏应该是平衡的。换句话说，有多少钱流出了赌场，就该有多少的钱流进赌场。既然赌场的钱最终被赢走了 2^(n+1) – 2 元，因此赌场的期望收入也就是 2^(n+1) – 2 元。而赌场收入的唯一来源是每人 1 元的初始赌金，这就表明游戏者的期望数量是 2^(n+1) – 2 个。换句话说，游戏平均进行了 2^(n+1) – 2 次。再换句话说，平均抛掷 2^(n+1) – 2 次硬币才会出现 n 连正的情况。

来自：这里