LeetCode动画 | 1038. 从二叉搜索树到更大和树

今天分享一个LeetCode题，题号是1038，标题是：从二分搜索树到更大和数。

题目描述

给出二叉搜索树的根节点，该二叉树的节点值各不相同，修改二叉树，使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

1）节点的左子树仅包含键小于节点键的节点。

2）节点的右子树仅包含键大于节点键的节点。

3）左右子树也必须是二叉搜索树。

示例：

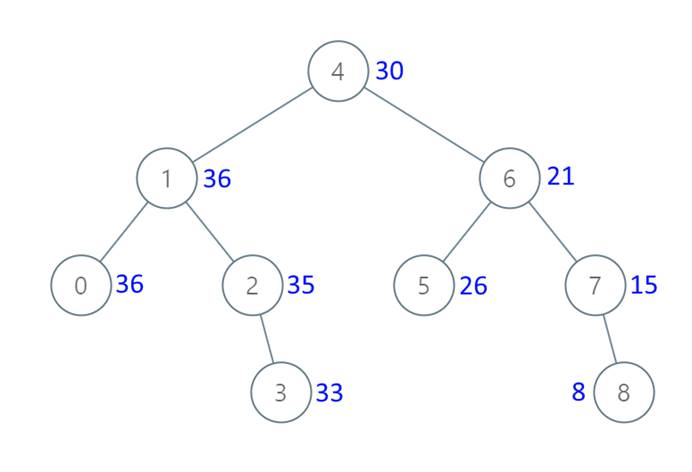
输入：[4, 1, 6, 0, 2, 5, 7, null, null, null, 3, null, null, null, 8]

输出：[30, 36, 21, 36, 35, 26, 15, null, null, null, 33, null, null, null, 8]

解题

光看题目描述，好像是看不到这题到底是什么意思，我反而是先看示例图就看懂了，你说气不气。

回归一下解题思路，这道题跟二分搜索树有关，之前也介绍过二分搜索树的遍历方式，如果需要回顾一下二分搜索数可以点击一下 传送 ，记得回城看题啊！

如果我们了解二分搜索树的中序遍历，求解这道题就变得非常容易。中序遍历是从左递归开始的，再进行访问这个节点，然后进行右递归，递归终止条件是这个节点为空。

看上面示例图，通过中序遍历可以得到有序数组：[0，1，2，3，4，5，6，7，8]，如果左右递归调换的话也可以得到倒序。

求解这道题正是通过右递归 -> 访问节点 -> 左递归，得到每一个节点的和数。执行动画如下视频：

动画

动画视频地址：点击

进行右递归时，一直到该节点为空，直接返回和数，和数起始为0；返回上一个节点，将当前和数与节点的值相加为新的和数，并且该节点赋值为新的和数；然后进行左递归进行下一个节点。

我们可以先设定一个和数int sum = 0;，你可以把它放到全局变量，也可以把它放到局部变量。放到局部变量时可以把它作为参数贯穿所有的节点。代码如下：

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode bstToGst(TreeNode root) {
        if(root == null) return null;
        int sum = 0;
        bstToGstInt(root,sum);
        return root;
    }

    public int bstToGstInt(TreeNode node,int sum){
        if(node == null) return sum;
        sum = bstToGstInt(node.right,sum);
        sum += node.val;
        node.val = sum;
        sum = bstToGstInt(node.left,sum);
        return sum;
    }
}

喜欢本文的朋友，欢迎关注公众号「算法无遗策」，收看更多精彩内容