LCA离线算法Tarjan详解

离线算法也就是需要先把所有查询给保存下来，最后一次输出结果。

离线算法是基于并查集实现的，首先就是初始化P[i] = i。

接下来对于每个点进行dfs：

①首先判断是否有与该点有关的查询，如果当前该点为u，与它有关的点为v，如果v已经访问过了，那么它们的LCA就是find（v）。如果v还没有访问，那就不用管它。

②对该点的子节点继续dfs，需要注意的是，dfs完之后需要需要p[v]=u，将v点并到其父亲节点上。

 void LCA(int u)
 {
     vis[u]=;
     for(int i=qhead[u];i!=-;i=query[i].next)
     {
         int v=query[i].v;
         if(vis[v] && !mark[Find(v)])  //mark数组是为了针对非连通图的情况
             ans[query[i].index]=Find(v);  //index次询问的公共祖先为Find（v）
     }

     for(int i=ehead[u];i!=-;i=e[i].next)
     {
         int v=e[i].v;
         if(!vis[v])
         {             LCA(v);
             p[v]=u;
         }
     }
 }

接下来详细解释一下为什么是这么一个原理：

对于任意两个节点u和v来说，它们只有两种关系：①子节点关系；②非子节点关系。

①子节点关系

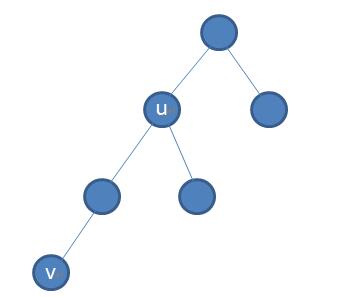
u和v的公共祖先很明显的就是u，在访问u结点的时候，v节点还没有被访问，此时继续访问u的子节点。那么当访问到v节点的时候，因为u节点已经被访问，所以此时u、v的LCA=find（u），由于此时p[u]=u，所以此时它们的LCA就是u。

②非子节点关系

此时u和v两个节点肯定有一个先访问，另一个后访问，现在就假设u先访问（v先访问的情况也是一样的）。

访问到u时，v还没有被访问，所以此时不用管，继续访问u的子节点，当u的子节点访问完之后，p[u] = f。

接下来访问到v时，由于u已经被访问，所以它们的LCA就是find（u），也就是p[f]=f，因为此时f的子节点还没有访问完，所以p[f]是不变的。

好了，两种情况都证明了。