HDU 3045 - Picnic Cows - [斜率DP]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3045

It’s summer vocation now. After tedious milking, cows are tired and wish to take a holiday. So Farmer Carolina considers having a picnic beside the river. But there is a problem, not all the cows consider it’s a good idea! Some cows like to swim in West Lake, some prefer to have a dinner in Shangri-la ,and others want to do something different. But in order to manage expediently, Carolina coerces all cows to have a picnic! 
Farmer Carolina takes her N (1<N≤400000) cows to the destination, but she finds every cow’s degree of interest in this activity is so different that they all loss their interests. So she has to group them to different teams to make sure that every cow can go to a satisfied team. Considering about the security, she demands that there must be no less than T(1<T≤N)cows in every team. As every cow has its own interest degree of this picnic, we measure this interest degree’s unit as “Moo~”. Cows in the same team should reduce their Moo~ to the one who has the lowest Moo~ in this team——It’s not a democratical action! So Carolina wishes to minimize the TOTAL reduced Moo~s and groups N cows into several teams. 
For example, Carolina has 7 cows to picnic and their Moo~ are ‘8 5 6 2 1 7 6’ and at least 3 cows in every team. So the best solution is that cow No.2,4,5 in a team (reduce (2-1)+(5-1) Moo~)and cow No.1,3,6,7 in a team (reduce ((7-6)+(8-6)) Moo~),the answer is 8. 

Input

The input contains multiple cases. 
For each test case, the first line has two integer N, T indicates the number of cows and amount of Safe-base line. 
Following n numbers, describe the Moo~ of N cows , 1st is cow 1 , 2nd is cow 2, and so on. 
Output

One line for each test case, containing one integer means the minimum of the TOTAL reduced Moo~s to group N cows to several teams.

Sample Input

7 3
8 5 6 2 1 7 6

Sample Output

8

题意：

现有N只奶牛，每只奶牛都有一个Moo[i]值，代表它对野餐的感兴趣程度；

现在要给奶牛们分成若干组，限定每组至少有t只奶牛；

每一组的奶牛的Moo值都会减少为其所在组的奶牛们中最小的Moo值。

题解：

首先对N只奶牛按照Moo值从小到大排序一下，重新编号为1~N；

设dp[i]代表前i项的minimize the TOTAL reduced Moo~s；

设sum[i]是Moo[]的前缀和数组；

则状态转移方程为dp[i] = min{ dp[j] + ( sum[i] - sum[j] ) - Moo[j+1] * ( i - j ) }，t ≤ j ≤ i - t；

可以看出要完成全部状态转移，是O(n²)的时间复杂度，N≤400000的范围，显然是要超时的，上斜率优化。

在计算dp[i]时，对于j的可能取值，假设有a,b，满足t ≤ a < b ≤ i - t，

若有dp[b] + ( sum[i] - sum[b] ) - Moo[b+1] * ( i - b ) ≤ dp[a] + ( sum[i] - sum[a] ) - Moo[a+1] * ( i - a )

则可以说b点优于a点；

对上式进行变形可得：

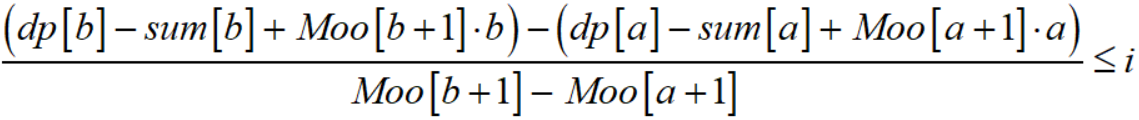
我们不妨设

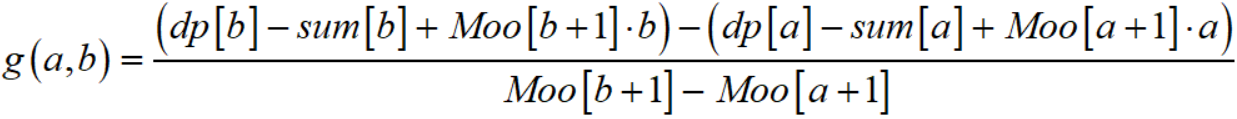
那么就有：

b点优于a点　<=>　g(a,b) ≤ i

b点劣于a点　<=>　g(a,b) > i

于是进一步的，就有：

在计算dp[i]时，对于j的可能取值，假设有a,b,c，满足t ≤ a < b < c ≤ i - t，

若g(a,b) ≥ g(b,c)，则b点必然淘汰。

证明：若g(b,c) ≤ i，则c点优于b点；若g(b,c) > i，则g(a,b) ≥ g(b,c) > i，则b点劣于a点；不管如何，b点都被淘汰。

再然后就是按照上面的性质，维护一个下凸的图形，斜率逐渐增大。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=+;
 
int n,t;
LL Moo[maxn],sum[maxn];
LL dp[maxn];
int q[maxn],head,tail;
 
LL up(int a,int b)
{
    return (dp[b]-sum[b]+Moo[b+]*b)-(dp[a]-sum[a]+Moo[a+]*a);
}
LL down(int a,int b)
{
    return Moo[b+]-Moo[a+];
}
 
int main()
{
    while(scanf("%d%d",&n,&t)!=EOF)
    {
        for(int i=;i<=n;i++) scanf("%I64d",&Moo[i]);
        sort(Moo+,Moo+n+);
        sum[]=;
        for(int i=;i<=n;i++) sum[i]=sum[i-]+Moo[i];
 
        head=tail=;
        dp[]=;
        for(int i=;i<=min(*t-,n);i++) dp[i]=dp[i-]+Moo[i]-Moo[];
 
        for(int i=*t;i<=n;i++)
        {
            int j=i-t;
            while(head+<tail)
            {
                int a=q[tail-], b=q[tail-];
                if(up(a,b)*down(b,j)>=up(b,j)*down(a,b)) tail--;
                else break;
            }
            q[tail++]=j;
 
            while(head+<tail)
            {
                int a=q[head], b=q[head+];
                if(up(a,b)<=i*down(a,b)) head++;
                else break;
            }
            j=q[head];
            dp[i]=dp[j]+(sum[i]-sum[j])-Moo[j+]*(i-j);
        }
 
        printf("%I64d\n",dp[n]);
    }
}

注意，本题Moo[i]没有明确说明范围，所以用int就爆掉了，要用long long，并且也不能直接g=up/down然后去比较g()，只能化成乘法形式。