BZOJ1045 [HAOI2008]糖果传递 && BZOJ3293 [Cqoi2011]分金币

Description

有n个小朋友坐成一圈，每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为1。

Input

第一行一个正整数nn<=1'000'000，表示小朋友的个数．

接下来n行，每行一个整数ai，表示第i个小朋友得到的糖果的颗数．

Output

求使所有人获得均等糖果的最小代价。

Sample Input

4
1
2
5
4

Sample Output

4

Solution

数学题

1045和3293是重题所以就放一起了，其实还有lrj蓝书上面的一道题也和这个一样（UVA的）

首先我们设每个人最后拥有的糖果数为$m$

那么很显然这个$m$是可以求出来的，$$m=\frac{\sum _{i=1}^{i<=n}A_i}{n}$$

再设一下，$xi$代表每个人传给了自己左边的人$xi$个糖果（对于$x1$，代表第一个人传给最后一个人$x1$个糖果（环形））

考虑第i个人，可以得到一个很显而易见的方程：$A_i - x_i + x_{i+1} = m$

为什么这个方程不用考虑左边的人传给这个人的情况？假设第$1$个人传给第$2$个人$3$个糖果，第$2$个人传给第$1$个人5个糖果，其实也就相当于，第$2$个人传给第$1$个人$2$个糖果，所以是不用考虑这个情况的（如果$1$传给$2$的牌比$2$传给$1$的多，那么$x2$则为负数）

同理可以得到一大堆的方程（其实就是把$1$~$n$分别代入上面的$i$）

我们可以尝试着解方程

然后会发现这方程是解不出来的

但是我们发现了一个点，可以拿x1表示这一大堆的其他的xi

现在我们设一个C数组，规定$C_i=C_{i-1}+A_i-m$

$a_1-x_1+x_2=m$化为$x_2=m-a_1+x_1=x_1-C_1$

同理，$a_2-x_2+x_3=m$化为

$x3$
$=m-a2+x2$
$=2*m-a2-a1+x1$
$=x1-C1-a2+m$
$=x1-C2$

于是我们就可以得到$n$个形似$xi=x1-Ci$的式子

好了我们在距离正解的路上已经迈出了一大步

考虑我们这$n-1$个等式能干啥

想想题目，我们想要传递的糖果数量尽可能少，也就是说，我们要让$\sum{abs(x)}$最小

然后再套一下之前的方程我们就可以把这个$\sum{abs(x)}$改写成$\sum{abs(x_1)+abs(x_1-C_1)+abs(x_2-C_2)···+abs(x_1-C_{n})}$

于是现在的问题就变成了，我们需要一个$x1$让$\sum{abs(x)}$最小

把这个玩意，映射到数轴上面，你就会发现一个神奇的东西

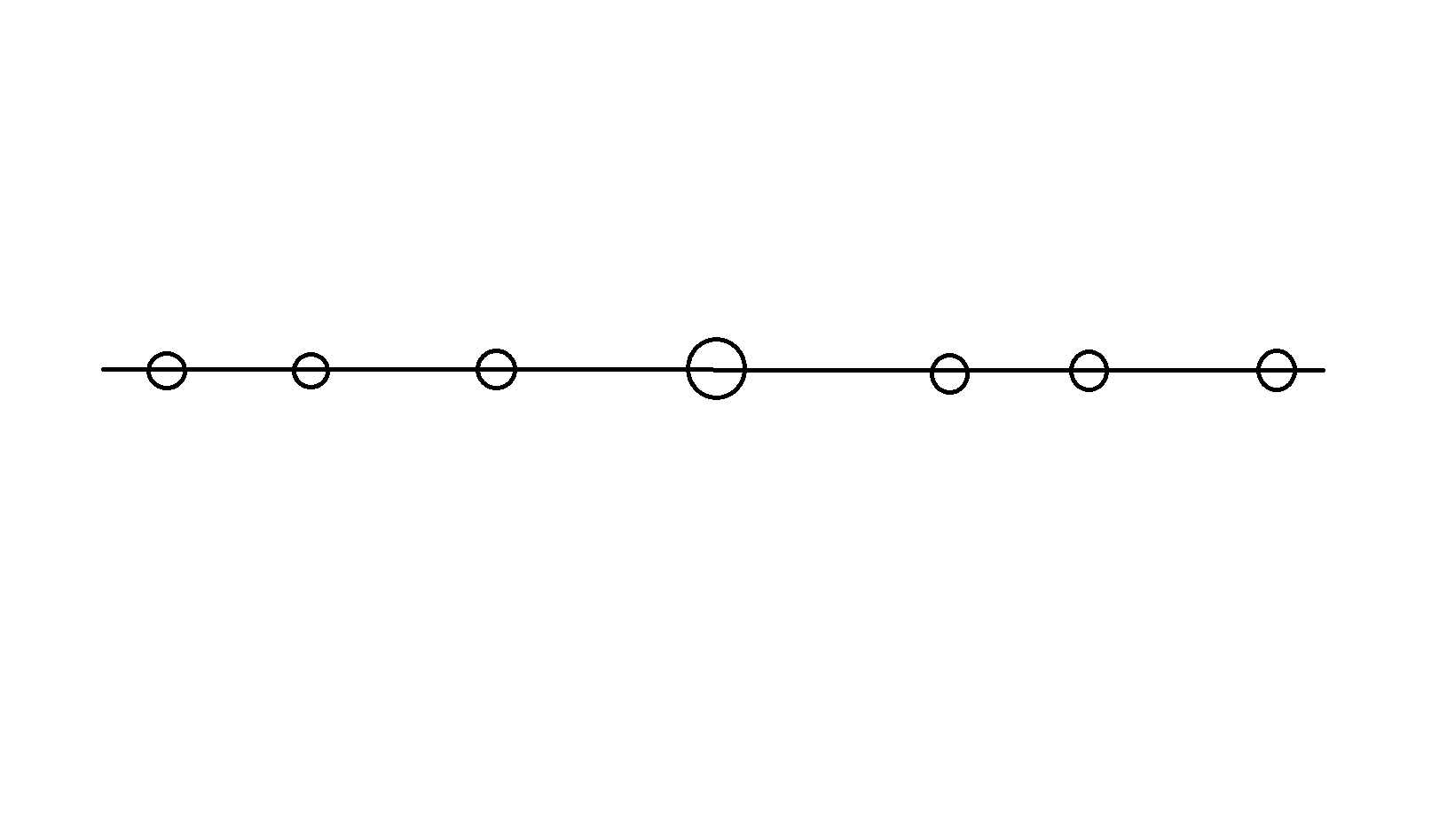
是的，就是中位数

怎么证明？

随便找一个点，假设这个点左边的点的数量多于右边的点的数量，那么肯定不是最优的，要向左移动（设它的左边有$l$个点，右边有$r$个点）（如果它向左移动了$t$个单位长度，假设还没碰到其他点，那么它距离左边的点少了$tl$的距离，距离右边多了$tr$的距离，总的距离事实上减少了$（l-r）t$个单位长度的距离，更优）

所以，使这个$\sum{abs(x)}$最小的$x_1$，一定会是$C$数组的中位数

所以得到这个$x1$之后，就可以推出这个$\sum{abs(x)}$的值了，答案也就出来了

嗯，这道题还卡$long \ long$，记得注意一下

挺好的一道数学题，挺思维的，代码难度也不大

#include <bits/stdc++.h>

using namespace std ;

#define ll long long
#define N 1000100

int n ;
ll a[ N ] , c[ N ] , sum =  , ans =  ;

int main() {
    scanf( "%d" , &n ) ;
    for( int i =  ; i <= n ; i ++ ) {
        scanf( "%lld" , &a[ i ] ) ;
        sum += a[ i ] ;
    }
    ll m = sum / n ;
    for( int i =  ;  i <= n ; i ++ ) {
        c[ i ] = c[ i -  ] + a[ i ] - m ;
    }
    sort( c +  , c + n +  ) ;
    ll t = c[ n &  ? ( n +  ) >>  : n >>  ] ;
    for( int i =  ; i <= n ; i ++ ) {
        ans += abs( c[ i ] - t ) ;
    }
    printf( "%lld\n" , ans ) ;
    return  ;
}