偏最小二乘回归(PLSR)- 1 概览
1. 概览
偏最小二乘算法,因其仅仅利用数据X和Y中部分信息(partial information)来建模,所以得此名字。其总体处理框架体现在下面两图中。
建议先看第2部分,对pls算法有初步了解后再看此框架,会有更全面深入的体会。
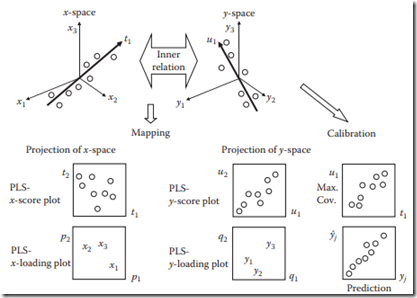 得到
得到

偏最小二乘回归(PLSR)- 1 概览的更多相关文章
- 【建模应用】PLS偏最小二乘回归原理与应用
@author:Andrew.Du 声明:本文为原创,转载请注明出处:http://www.cnblogs.com/duye/p/9031511.html,谢谢. 一.前言 1.目的: 我写这篇文章的 ...
- 偏最小二乘回归(PLSR)- 2 标准算法(NIPALS)
1 NIPALS 算法 Step1:对原始数据X和Y进行中心化,得到X0和Y0.从Y0中选择一列作为u1,一般选择方差最大的那一列. 注:这是为了后面计算方便,如计算协方差时,对于标准化后的数据,其样 ...
- 【数学建模】偏最小二乘回归分析(PLSR)
PLSR的基本原理与推导,我在这篇博客中有讲过. 0.偏最小二乘回归集成了多元线性回归.主成分分析和典型相关分析的优点,在建模中是一个更好的选择,并且MATLAB提供了完整的实现,应用时主要的问题是: ...
- [matlab] 21.灰色预测、线性回归分析模型与最小二乘回归 (转载)
灰色预测的主要特点是只需要4个数据,就能解决历史数据少,序列的完整性以及可靠性低的问题,能将无规律的原始数据进行生成得到规律性较强的生成序列,易于检验 但缺点是只适合中短期的预测,且只适合指数级增长的 ...
- 偏最小二乘回归分析建模步骤的R实现(康复俱乐部20名成员测试数据)+补充pls回归系数矩阵的算法实现
kf=read.csv('d:/kf.csv') # 读取康复数据kfsl=as.matrix(kf[,1:3]) #生成生理指标矩阵xl=as.matrix(kf[,4:6]) #生成训练指标矩阵x ...
- 一般多项式曲线的最小二乘回归(Linear Regression)
对于一般多项式: K为多项式最高项次,a为不确定的常数项,共k+1个; 有离散数据集对应,其方差: β为,方差函数S对β自变量第j个参数的梯度(偏导数): 当以上梯度为零时,S函数值最小,即: 中的每 ...
- 【cs229-Lecture2】Gradient Descent 最小二乘回归问题解析表达式推导过程及实现源码(无需迭代)
视频地址:http://v.163.com/movie/2008/1/B/O/M6SGF6VB4_M6SGHJ9BO.html 机器学习课程的所有讲义及课后作业:http://pan.baidu.co ...
- 岭回归和lasso回归(转)
回归和分类是机器学习算法所要解决的两个主要问题.分类大家都知道,模型的输出值是离散值,对应着相应的类别,通常的简单分类问题模型输出值是二值的,也就是二分类问题.但是回归就稍微复杂一些,回归模型的输出值 ...
- 在线场景感知:图像稀疏表示—ScSPM和LLC总结(以及lasso族、岭回归)
前言: 场景感知其实不分三维场景和二维场景,可以使用通用的方法,不同之处在于数据的形式,以及导致前期特征提取及后期在线场景分割过程.场景感知即是场景语义分析问题,即分析场景中物体的特征组合与相应场景的 ...
随机推荐
- C# 时间戳与当前时间互相转换
时间戳: Unix时间戳(Unix timestamp),或称Unix时间(Unix time).POSIX时间(POSIX time),是一种时间表示方式,定义为从格林威治时间1970年01月01日 ...
- PAT甲级1049. Counting Ones
PAT甲级1049. Counting Ones 题意: 任务很简单:给定任何正整数N,你应该计算从1到N的整数的十进制形式的1的总数.例如,给定N为12,在1,10, 11和12. 思路: < ...
- 把json格式的字符串转换成javascript对象或数组
第一种 JSON.parse(jsonString) 第二种 eval("("+jsonString+")") 第三种 var obj=(function ...
- UIColor和 同 CIColor 与 CGColor 之间的联系、转换
1. 利用UIColor展现 #F6F6F6 这个传统的颜色 #F6F6F6 为一个 16 进制表示的RPG颜色,所以,需要先转换成 10进制,其中 F6 - 240,F6 - 240 ,F6 - ...
- mysql知识点(三)
1.表关联是可以利用两个表的索引的,如果是用子查询,至少第二次查询是没有办法使用索引的. 2. 为了给主查询提供数据而首先执行的查询被叫做子查询 3.如果WHERE子句的查询条件里使用了函数(WHE ...
- FAQ:Domain Event 和 C# 中的 Event 有啥区别?
问: Domain Event 和 C# 中的 Event 有啥区别? 答: C# 中的 Event,事件.监听者列表和事件发布器是由一个类型承担,事件源和监听者之间的生命周期耦合在一起,C# 帮你提 ...
- [Android Pro] git 打标签、推送tag到托管服务器、验证是否成功
reference to : http://www.cnblogs.com/ShaYeBlog/p/5576601.html 我们常常在代码封板时,使用git 创建一个tag ,这样一个不可修改的历史 ...
- datagridview 纵向 横向 合并单元格
datagridview 单元格合并:纵向以及横向合并参考了csdn上不知哪位的代码,具体哪位找不到连接了. 纵向合并: /// <summary> /// 纵向合并,即合并数据项的值 / ...
- SRM 212 Div II Level Two: WinningRecord,Brute Force
题目来源:http://community.topcoder.com/stat?c=problem_statement&pm=3003&rd=5858 比较简单. 代码如下: #inc ...
- C# SMTP邮件发送程序
邮件发送在网站应用程序中经常会用到,包括您现在看到的博客,在添加评论后,系统会自动发送邮件通知到我邮箱的,把系统发送邮件的功能整理了下,做了一个客户端Demo,希望对有需要的童鞋有所帮助: 核心代码: ...
