HDU 4423 Simple Function（数学题，2012长春D题）

Simple Function

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 111    Accepted Submission(s): 31

Problem Description

Knowing that x can be any real number that x² + Dx + E ≠ 0. Now, given the following function:

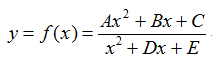
What is the range of y?

 

Input

The first line contains a single integer T (T ≤ 10000), indicating that there are T cases below.
Each case contains five integers in a single line which are values of A, B, C, D and E (-100 ≤ A, B, C, D, E ≤ 100).

 

Output

For each case, output the range of y in the form of standard interval expression like in a single line.
The expression is made up by one interval or union of several disjoint intervals.
Each interval is one of the following four forms: "(a, b)", "(a, b]", "[a, b)", "[a, b]"(there is a single space between ',' and 'b'), where a, b are real numbers rounded to 4 decimal places, or "-INF" or "INF" if the value is negative infinity or positive infinity.
If the expression is made up by several disjoint intervals, put the letter 'U' between adjacent intervals. There should be a single space between 'U' and nearby intervals.
In order to make the expression unique, the expression should contain as minimum of intervals as possible and intervals should be listed in increasing order.
See sample output for more detail.

 

Sample Input

5
1 1 1 2 3
0 1 0 1 -10
-3 -1 0 -1 -1
0 0 0 0 0
1 3 0 2 0

 

Sample Output

[0.3170, 1.1830]
(-INF, INF)
(-INF, -1.8944] U [-0.1056, INF)
[0.0000, 0.0000]
(-INF, 1.0000) U (1.0000, 1.5000) U (1.5000, INF)

 

Source

2012 Asia ChangChun Regional Contest

 

Recommend

zhuyuanchen520

 

2012长春的D题，当年只有两个队过，够坑的。

其实就是讨论的情况比较多，折腾了一天终于分析清楚了，还debug了好久。

我是把分母乘过来分析的。

另外一种分析方法见：

http://blog.happybin.org/archives/zoj_3658_simple-function_2012_changchun_site/

我的做法：

代码：

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013-10-5 12:05:22
 File Name     :E:\2013ACM\专题强化训练\区域赛\2012长春\D.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;
 const double eps = 1e-;
 int main()
 {
     //freopen("d.in","r",stdin);
     //freopen("out.txt","w",stdout);
     int A,B,C,D,E;
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d%d%d%d",&A,&B,&C,&D,&E);
         if(B == D*A && C == E*A)
         {
             printf("[%.4lf, %.4lf]\n",1.0*A,1.0*A);
             continue;
         }
         bool fA;//值域包不包含A
         if(B == D*A)fA = false;
         else
         {
             /*
             double ttx = (double)(E*A-C)/(B-D*A);
             if(fabs(ttx*ttx + D*ttx + E) < eps)fA = false;
             else fA = true;
             */
             int t1 = E*A - C;
             int t2 = B-D*A;
             if((long long)t1*t1 +(long long)D*t2*t1 +(long long)E*t2*t2 == )fA = false;
             else fA = true;
         }
         if(D*D < *E)
         {
             int a = D*D - *E;
             int b = *A*E + *C - *B*D;
             int c = B*B - *A*C;
             double l = (-b+sqrt(1.0*b*b-4.0*a*c))/(2.0*a);
             double r = (-b-sqrt(1.0*b*b-4.0*a*c))/(2.0*a);
             if(B != D*A)
             {
                 if(fA)printf("[%.4lf, %.4lf]\n",l,r);
                 else printf("[%.4lf, %.4lf) U (%.4lf, %.4lf]\n",l,1.0*A,1.0*A,r);
             }
             else
             {
                 if(fabs(A-l) < eps)printf("(%.4lf, %.4lf]\n",l,r);
                 else printf("[%.4lf, %.4lf)\n",l,r);
             }
             continue;
         }
         if(D*D == *E)
         {
             int f1 = *A*E + *C - *B*D;
             double tt1 = (-D)/(2.0);
             if(f1 == )//
             {
                 if(B*B > *A*C)
                 {
                     if(fA)printf("(-INF, INF)\n");
                     else printf("(-INF, %.4lf) U (%.4lf, INF)\n",1.0*A,1.0*A);
                 }
                 else while();//****
                 //while(1);
             }
             else if(f1 > )
             {
                 double l = (double)(-B*B + *A*C)/f1;
                 double tt2 = -(B-D*l)/(*A - *l);
                 if(fabs(tt2 - tt1) < eps)
                 {
                     if(!fA)
                     {
                         if(B != D*A)
                             printf("(%.4lf, %.4lf) U (%.4lf, INF)\n",l,1.0*A,1.0*A);
                         else printf("(%.4lf, INF)\n",l);
                     }
                     else printf("(%.4lf, INF)\n",l);
                 }
                 else
                 {
                     if(!fA)
                     {
                         if(B == D*A)printf("(%.4lf, INF)\n",l);
                         else printf("[%.4lf, %.4lf) U (%.4lf, INF)\n",l,1.0*A,1.0*A);
                     }
                     else printf("[%.4lf, INF)\n",l);
                 }
             }
             else
             {
                 double r = (double)(-B*B + *A*C)/f1;
                 double tt2 = -(B-D*r)/(*A - *r);
                 if(fabs(tt2 - tt1) < eps)
                 {
                     if(!fA)
                     {
                         if(B != D*A)
                             printf("(-INF, %.4lf) U (%.4lf, %.4lf)\n",1.0*A,1.0*A,r);
                         else printf("(-INF, %.4lf)\n",r);
                     }
                     else printf("(-INF, %.4lf)\n",r);
                 }
                 else
                 {
                     if(!fA)
                     {
                         if(B == D*A)printf("(-INF, %.4lf)\n",r);
                         else printf("(-INF, %.4lf) U (%.4lf, %.4lf]\n",1.0*A,1.0*A,r);
                     }
                     else printf("(-INF, %.4lf]\n",r);
                 }
             }
             continue;
         }
         if(D*D > *E)
         {
             double root1 = (double)(-D + sqrt(D*D - *E) )/;
             double root2 = (double)(-D - sqrt(D*D - *E))/;
             int a = D*D - *E;
             int b = *A*E + *C - *B*D;
             int c = B*B - *A*C;
             long long deta = (long long)b*b - (long long)*a*c;
             if(deta < )
             {
                 if(fA)printf("(-INF, INF)\n");
                 else printf("(-INF, %.4lf) U (%.4lf, INF)\n",1.0*A,1.0*A);
             }
             else if(deta == )
             {
                 double y0 = (double)(-b)/(*a);
                 double tt2 = (double)(D*y0 - B)/(*(A-y0));
                 if(fabs(tt2 - root1) < eps || fabs(tt2 - root2) < eps)
                 {
                     if(!fA && A < y0 - eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf) U (%.4lf, INF)\n",(double)A,(double)A,y0,y0);
                     else if(!fA && A > y0+eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf) U (%.4lf, INF)\n",y0,y0,(double)A,(double)A);
                     else printf("(-INF, %.4lf) U (%.4lf, INF)\n",y0,y0);
                 }
                 else
                 {
                     if(!fA)
                         printf("(-INF, %.4lf) U (%.4lf, INF)\n",(double)A,(double)A);
                     else printf("(-INF, INF)\n");
                 }
             }
             else
             {
                 double y1 = (double)(-b-sqrt(1.0*b*b-4.0*a*c))/(*a);
                 double y2 = (double)(-b+sqrt(1.0*b*b-4.0*a*c))/(*a);
                 double tt1 = (double)(D*y1 - B)/(*(A-y1));
                 double tt2 = (double)(D*y2 - B)/(*(A-y2));
                 bool fy1 = true;
                 bool fy2 = true;
                 if(fabs(tt1 - root1) < eps || fabs(tt1 - root2) < eps)
                     fy1 = false;
                 if(fabs(tt2 - root1) < eps || fabs(tt2 - root2) < eps)
                     fy2 = false;
                 if(!fA && fabs(y1 - A) < eps)fy1 = false;
                 if(!fA && fabs(y2 - A) < eps)fy2 = false;
                 if(fy1 && fy2)
                 {
                     if(!fA && A < y1 - eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf] U [%.4lf, INF)\n",(double)A,(double)A,y1,y2);
                     else if(!fA && A > y2 + eps)
                         printf("(-INF, %.4lf] U [%.4lf, %.4lf) U (%.4lf, INF)\n",y1,y2,(double)A,(double)A);
                     else printf("(-INF, %.4lf] U [%.4lf, INF)\n",y1,y2);
                 }
                 else if(fy1 && !fy2)
                 {
                     if(!fA && A < y1 - eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf] U (%.4lf, INF)\n",(double)A,(double)A,y1,y2);
                     else if(!fA && A > y2 + eps)
                         printf("(-INF, %.4lf] U (%.4lf, %.4lf) U (%.4lf, INF)\n",y1,y2,(double)A,(double)A);
                     else printf("(-INF, %.4lf] U (%.4lf, INF)\n",y1,y2);
                 }
                 else if(!fy1 && fy2)
                 {
                     if(!fA && A < y1 - eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf) U [%.4lf, INF)\n",(double)A,(double)A,y1,y2);
                     else if(!fA && A > y2 + eps)
                         printf("(-INF, %.4lf) U [%.4lf, %.4lf) U (%.4lf, INF)\n",y1,y2,(double)A,(double)A);
                     else printf("(-INF, %.4lf) U [%.4lf, INF)\n",y1,y2);
                 }
                 else
                 {
                     if(!fA && A < y1 - eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf) U (%.4lf, INF)\n",(double)A,(double)A,y1,y2);
                     else if(!fA && A > y2 + eps)
                         printf("(-INF, %.4lf) U (%.4lf, %.4lf) U (%.4lf, INF)\n",y1,y2,(double)A,(double)A);
                     else printf("(-INF, %.4lf) U (%.4lf, INF)\n",y1,y2);
                 }
             }
         }
     }
     return ;
 }