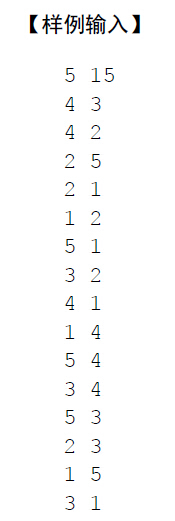[清华集训2015 Day1]主旋律-[状压dp+容斥]
Description

Solution
f[i]表示状态i所代表的点构成的强连通图方案数。
g[i]表示状态i所代表的的点形成奇数个强连通图的方案数-偶数个强连通图的方案数。
g是用来容斥的。
先用f更新g。枚举状态i的编号最小点k所在连通块大小i-j,$g[i]=-\sum _{j\subset i}f[i-j]*g[j]$(此处g中不更新强连通图个数为1的。
设点集i中有sum条边,则:
$f[i]=2^{sum}-\sum _{j\subset i}2^{sum-w[j]}*g[j]$。其中w[j]是i射向j的边数,这些边被钦定不能选。
最后记得用f[i]更新g[i]。
Code
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int mod=1e9+;
int n,m,x,y;
int in[],out[];
int num[],sum[];
ll f[],g[],bin[],w[];
void calw(int s,int c)
{
if (!c) return;
calw(s,(c-)&s);
w[c]=w[c^(c&-c)]+num[in[c&-c]&s];
}
int main()
{
scanf("%d%d",&n,&m);
bin[]=;for (int i=;i<=m;i++) bin[i]=(bin[i-]<<)%mod;
for (int i=;i<=m;i++)
{
scanf("%d%d",&x,&y);x--;y--;
in[bin[y]]|=bin[x];
out[bin[x]]|=bin[y];
}
for (int i=;i<bin[n];i++) for (int j=;j<n;j++)
if (i&bin[j]) num[i]++; for (int i=;i<bin[n];i++)
{
int lowbit=i&-i,s=i^lowbit;
for (int j=s;j;j=s&(j-)) g[i]=(g[i]-f[j^i]*g[j]%mod)%mod; sum[i]=sum[s]+num[in[lowbit]&s]+num[out[lowbit]&s];
f[i]=bin[sum[i]];
calw(i,i); for (int j=i;j;j=i&(j-))
{
f[i]=(f[i]-bin[sum[i]-w[j]]*g[j]%mod+mod)%mod;
}
g[i]+=f[i];if (g[i]>=mod) g[i]%=mod;
}
cout<<f[bin[n]-]; }
[清华集训2015 Day1]主旋律-[状压dp+容斥]的更多相关文章
- BZOJ 3812 主旋律 (状压DP+容斥) + NOIP模拟赛 巨神兵(obelisk)(状压DP)
这道题跟另一道题很像,先看看那道题吧 巨神兵(obelisk) 题面 欧贝利斯克的巨神兵很喜欢有向图,有一天他找到了一张nnn个点mmm条边的有向图.欧贝利斯克认为一个没有环的有向图是优美的,请问这张 ...
- codeforces 342D Xenia and Dominoes(状压dp+容斥)
转载请注明出处: http://www.cnblogs.com/fraud/ ——by fraud D. Xenia and Dominoes Xenia likes puzzles ...
- bzoj2669 [cqoi2012]局部极小值 状压DP+容斥
题目传送门 https://lydsy.com/JudgeOnline/problem.php?id=2669 题解 可以发现一个 \(4\times 7\) 的矩阵中,有局部最小值的点最多有 \(2 ...
- 一本通 1783 矩阵填数 状压dp 容斥 计数
LINK:矩阵填数 刚看到题目的时候感觉是无从下手的. 可以看到有n<=2的点 两个矩形. 如果只有一个矩形 矩形外的方案数容易计算考虑 矩形内的 必须要存在x这个最大值 且所有值<=x. ...
- P3160 [CQOI2012]局部极小值 题解(状压DP+容斥)
题目链接 P3160 [CQOI2012]局部极小值 双倍经验,双倍快乐 解题思路 存下来每个坑(极小值点)的位置,以这个序号进行状态压缩. 显然,\(4*7\)的数据范围让极小值点在8个以内(以下示 ...
- HDU 5838 (状压DP+容斥)
Problem Mountain 题目大意 给定一张n*m的地图,由 . 和 X 组成.要求给每个点一个1~n*m的数字(每个点不同),使得编号为X的点小于其周围的点,编号为.的点至少大于一个其周围的 ...
- uoj#37. 【清华集训2014】主旋律(状压dp+容斥)
传送门 第一眼容斥,然后我就死活容不出来了-- 记\(f_i\)为点集\(i\)中的点强联通的方案数,那么就是总的方案数减去使\(i\)不连通的方案数 如果\(i\)不连通的话,我们可以枚举缩点之后拓 ...
- bzoj2560串珠子 状压dp+容斥(?)
2560: 串珠子 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 515 Solved: 348[Submit][Status][Discuss] ...
- NOIp模拟赛 巨神兵(状压DP 容斥)
\(Description\) 给定\(n\)个点\(m\)条边的有向图,求有多少个边集的子集,构成的图没有环. \(n\leq17\). \(Solution\) 问题也等价于,用不同的边集构造DA ...
随机推荐
- Hive 锁 lock
Hive + zookeeper 可以支持锁功能 锁有两种:共享锁.独占锁,Hive开启并发功能的时候自动开启锁功能 1)查询操作使用共享锁,共享锁是可以多重.并发使用的 2)修改表操作使用独占锁,它 ...
- Oracle EBS 用户职责人员取值
SELECT fu.user_name 用户名, fu.description 用户说明, fu.start_date 用户启用日期, fu.end_date 用户终止日期 --,fu.employe ...
- SEO-搜索引擎优化
一.定义 SEO(Search Engine Optimization):汉译为搜索引擎优化.是一种方式:利用搜索引擎的规则提高网站在有关搜索引擎内的自然排名.目的是:为网站提供生态式的自我营销解决方 ...
- Coursera-AndrewNg(吴恩达)机器学习笔记——第四周
神经网络 1.神经网络发展的动力:在逻辑回归解决复杂的分类问题时,我们使用属性的一些组合来构造新的属性(x12,x1x2,x22...),这样就会造成属性的数目n过多,带来了大量的运算,甚至造成过拟合 ...
- mysql 5.7.16 忘记root 密码 如何修改root密码
今天在电脑上安装 mysql5.7.16 (压缩包)时,在初始化data文件夹之后,没有记住密码,DOS框没有显示,没办法,为了学习一下怎么修改密码,在网上找了好多方法去解决,最终还是解决了,下面来 ...
- 乘风破浪:LeetCode真题_029_Divide Two Integers
乘风破浪:LeetCode真题_029_Divide Two Integers 一.前言 两个整数相除,不能使用乘法除法和取余运算.那么就只能想想移位运算和加减法运算了. 二.Divide T ...
- [ML学习笔记] 决策树与随机森林(Decision Tree&Random Forest)
[ML学习笔记] 决策树与随机森林(Decision Tree&Random Forest) 决策树 决策树算法以树状结构表示数据分类的结果.每个决策点实现一个具有离散输出的测试函数,记为分支 ...
- window与Linux之间的文件传输
使用工具:WinSCP WinSCP可以直接通过SSH链接你的linux服务器:然后进行文件的复制操作:并且可以直接编辑文件. 1.下载WinSCP 2.登录WinSCP,输入你的Linux 的IP地 ...
- Android (争取做到)最全的底部导航栏实现方法
本文(争取做到)Android 最全的底部导航栏实现方法. 现在写了4个主要方法. 还有一些个人感觉不完全切题的方法也会简单介绍一下. 方法一. ViewPager + List<View> ...
- Python中让MySQL查询结果返回字典类型的方法
import pymysql host='localhost' user='root' passwd='root' port=3306 db='test' db=pymysql.connect( ho ...