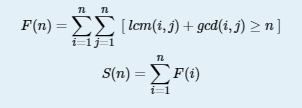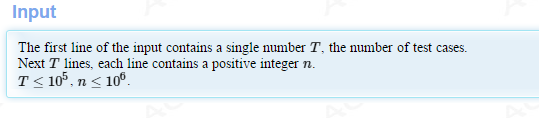【HDU 5382】 GCD?LCM! (数论、积性函数)
GCD?LCM!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 316 Accepted Submission(s): 200
OutputT lines, find S(n) mod 258280327.Sample Input8
1
2
3
4
10
100
233
11037Sample Output1
5
13
26
289
296582
3928449
213582482AuthorSXYZSource
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define Maxn 1000010
#define Mod 258280327 int pri[Maxn],pl,g[Maxn],t[Maxn],f[Maxn];
bool vis[Maxn]; void init()
{
memset(vis,,sizeof(vis));
pl=;g[]=;
for(int i=;i<=Maxn-;i++)
{
if(!vis[i]) pri[++pl]=i,g[i]=;
for(int j=;j<=pl;j++)
{
if(pri[j]*i>Maxn-) break;
vis[i*pri[j]]=;
if(i%pri[j]==) g[i*pri[j]]=g[i];
else g[i*pri[j]]=*g[i]%Mod;
if(i%pri[j]==) break;
}
}
for(int i=;i<=Maxn-;i++)
{
for(int j=i;j<=Maxn-;j+=i)
{
t[j]=(t[j]+g[j/i-])%Mod;
}
}
for(int i=;i<=Maxn-;i++) f[i]=(f[i-]+(*i-)-t[i-])%Mod;
for(int i=;i<=Maxn-;i++) f[i]=((f[i]+f[i-])%Mod+Mod)%Mod;
} int main()
{
init();
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
printf("%d\n",f[n]);
}
return ;
}
【有一点点容斥的东东在么?】
2017-04-27 15:28:52
【HDU 5382】 GCD?LCM! (数论、积性函数)的更多相关文章
- 2015多校第8场 HDU 5382 GCD?LCM! 数论公式推导
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5382 题意:函数lcm(a,b):求两整数a,b的最小公倍数:函数gcd(a,b):求两整数a,b的最 ...
- 数学--数论--Hdu 1452 Happy 2004(积性函数性质+和函数公式+快速模幂+乘法逆元)
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your ...
- hdu 5382 GCD?LCM! - 莫比乌斯反演
题目传送门 传送门I 传送门II 题目大意 设$F(n) = \sum_{i = 1}^{n}\sum_{j = 1}^{n}\left [ [i, j] + (i, j) \geqslant n \ ...
- hdu 5382 GCD?LCM!
先考虑化简f函数 发现,f函数可以写成一个递归式,化简后可以先递推求出所有f函数的值, 所以可以先求出所有S函数的值,对于询问,O(1)回答 代码: //File Name: hdu5382.cpp ...
- 积性函数,线性筛入门 HDU - 2879
HDU - 2879HeHe 题意:He[N]为[0,N−1]范围内有多少个数满足式子x2≡x (mod N),求HeHe[N]=He[1]×……×He[N] 我是通过打表发现的he[x]=2k,k为 ...
- 数学--数论--HDU 5382 GCD?LCM?(详细推导,不懂打我)
Describtion First we define: (1) lcm(a,b), the least common multiple of two integers a and b, is the ...
- HDU 1452 Happy 2004 (逆元+快速幂+积性函数)
G - Happy 2004 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Subm ...
- HDU 1452 Happy 2004(因子和的积性函数)
题目链接 题意 : 给你一个X,让你求出2004的X次方的所有因子之和,然后对29取余. 思路 : 原来这就是积性函数,点这里这里这里,这里讲得很详细. 在非数论的领域,积性函数指所有对于任何a,b都 ...
- Mobius反演与积性函数前缀和演学习笔记 BZOJ 4176 Lucas的数论 SDOI 2015 约数个数和
下文中所有讨论都在数论函数范围内开展. 数论函数指的是定义域为正整数域, 且值域为复数域的函数. 数论意义下的和式处理技巧 因子 \[ \sum_{d | n} a_d = \sum_{d | n} ...
随机推荐
- POJ - 3436 ACM Computer Factory(最大流)
https://vjudge.net/problem/POJ-3436 题目描述: 正如你所知道的,ACM 竞赛中所有竞赛队伍使用的计算机必须是相同的,以保证参赛者在公平的环境下竞争.这就是所有这些 ...
- inline-block的间距问题
张鑫旭的博客有提到,解决的方法有很多,先贴下,回头再做整理. http://www.zhangxinxu.com/wordpress/2012/04/inline-block-space-remove ...
- js 正则学习小记之匹配字符串字面量
今天看了第5章几个例子,有点收获,记录下来当作回顾也当作分享. 关于匹配字符串问题,有很多种类型,今天讨论 js 代码里的字符串匹配.(因为我想学完之后写个语法高亮练手,所以用js代码当作例子) va ...
- HTML的文档类型:<!DOCTYPE >
<!DOCTYPE> 声明:它不是 HTML 标签而且对大小写不敏感,而是指示 web 浏览器关于页面使用哪个 HTML 版本进行编写的指令.而且 声明必须是 HTML 文档的第一行,位于 ...
- Value = undefined
Value = undefined Javascript在计算机程序中,经常会声明无值的变量.未使用值来声明的变量,其值实际上是 undefined. 在执行过以下语句后,变量 carname 的值将 ...
- sequelize初使用
官网地址:Sequelize Sequelize is a promise-based ORM for Node.js v4 and up. It supports the dialects Post ...
- mybatis多对多关联查询——(十)
1.需求 查询用户及用户购买商品信息. 2 sql语句 查询主表是:用户表 关联表:由于用户和商品没有直接关联,通过订单和订单明细进行关联,所以关联表: orders.orderdetail. ...
- Valid Parentheses & Longest Valid Parentheses
Valid Parentheses Given a string containing just the characters '(', ')', '{', '}', '[' and ']', det ...
- maven:多个镜像配置
<mirrors> <mirror> <id>nexus-aliyun</id> <mirrorOf>nexus-aliyun</mi ...
- Python api认证
本节内容: 基本的api 升级的api 终极版api 环境:Djanao, 项目名:api_auto, app:api 角色:api端,客户端,黑客端 1.基本的api [api端] #api_aut ...