利用KMP算法解决串的模式匹配问题（c++) -- 数据结构

题目：

7-1 串的模式匹配 （30 分)

给定一个主串S（长度<=10^6）和一个模式T（长度<=10^5），要求在主串S中找出与模式T相匹配的子串，返回相匹配的子串中的第一个字符在主串S中出现的位置。

输入格式:

输入有两行： 第一行是主串S； 第二行是模式T.

输出格式:

输出相匹配的子串中的第一个字符在主串S中出现的位置。若匹配失败，输出0.

输入样例:

在这里给出一组输入。例如：

aaaaaba
ba

输出样例:

在这里给出相应的输出。例如：

6

---

分析：

这里就是在主串里面找是否存在和模式串相等的子串啦,
如果存在就输出该子串在主串中第一个字符的位置，否则输出0。

主要有两种方法：

1.BF算法(在数据量大的时候可能会导致运行超时）

2.KMP算法

这里将采用KMP算法

---

代码：

#include<iostream>
#include<string.h>
using namespace std;

/*在本题中有如例题般屈指可数的字符串，也有10^6如此庞大的数据，
为了避免不必要的空间浪费，笔者决定在输入字符串string s后
化为字符数组 char *s[s.length()]

为此，我还特地查找了string的最大容量：
堆开得足够大，数组的最大长度是可以不断增大的（推测最长的长度为 2^32，也就是4G。)
但编码时有需要注意的地方，采用明文的方式，如果超过65534个字节，可能报编译错误。
*/ 

char* trans(string str)
{
    int size = str.length();
    char *s;
    s= new char[size];
    strcpy(s, str.c_str());
    return s;
}

void calc_next(string pstring, int *next)
{
    next[] = -;//-1表示模式串开头
    int j = , k = -;
    int p_len = pstring.length();//模式串长度
    char *p = trans(pstring);//模式串字符数组

    while(j<p_len){//当j尚未指向模式串尾端时
        if(k == - || p[j] == p[k]) {
            k++;//k指前缀开始下标
            j++;//j指后缀开始下标
            next[j] = k;//next[]存放已匹配子串中最长前后缀长度
            //其中，next[j]表示 p[0]-p[j-1]子串中最长前后缀长度
        }else{
            k = next[k]; //k回溯到模式串开头
        }
    }
}

int kmp(string sstring, string pstring)
{
    int *next = new int[pstring.length()];
    calc_next(pstring, next);//得到 next[]数组
    char *s = trans(sstring), *p = trans(pstring); //转字符串为字符数组
    int i=, j=;
    int pos = ;

    while( i<=sstring.length() || j<=pstring.length()){
        if( j == - || s[i] == p[j]){
            i++;
            j++;
        }else{
            j = next[j];
            /*
            ①有最长前后缀时：
              当主串和模式串在主串s[j]位置(即模式串最长后缀后一位）
            不匹配时， s[j]将和 模式串最长前缀后一位比较
            ②冇最长前后缀时：
              j = next[0] == -1;
            整个模式串向后移一位
            */
        }

        if(j == pstring.length()){//匹配成功
            pos = i-j+;
            break;
        }
    } 

    return pos;

} 

int main()
{
    string sstring, pstring;//定义字符串
    getline(cin, sstring);//输入字符串
    getline(cin, pstring);

    cout<<kmp(sstring, pstring);
    return ;

}

2019.04.07  22:08更新

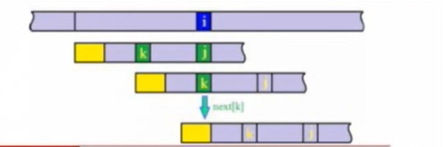
继续查阅资料的时候发现了一个可以优化原始KMP算法的判断条件：

以上图为例

我们的模式串 p[j] 是与主串中 s[i] 不匹配时才开始第一次移位，但是我们发现有一种情况：

模式串中的 p[k] == p[j] ，p[j] != s[i] ；由此我们可以知道 p[k] != s[i] ，那么这时我们需要进行第二次移位。

针对上述情况，不妨在第一次移位前增加一个判断条件，即当  p[j] == p[k] 时令 next[j] = next[k] ，如此便可一步到位，优化算法。

部分代码更改如下：

    while(j<p_len){//当j尚未指向模式串尾端时
        if(k == - || p[j] == p[k]) {
            k++;//k指前缀开始下标
            j++;//j指后缀开始下标
            if(p[j] == p[k]){
                next[j] = next[k];
            }else{
                next[j] = k;//next[]存放已匹配子串中最长前后缀长度
            //其中，next[j]表示 p[0]-p[j-1]子串中最长前后缀长度
            }

        }else{
            k = next[k]; //k回溯到模式串开头
        }
    }

---

编程中遇到的困难：

1.KMP算法相对于BF算法或者时其他算法来说更为抽象，没有办法很好地从利用该算法的目的、优势、所需操作方法等内容正向理解。
  需要从KMP核心原理入手才能够感悟到数据结构之美。

2.值得注意的一点是（部分博客没有说清楚）我们所求的最长前后缀是在已经匹配的模式串子串中，而非整个模式串，更非主串。

---

总结：

  在实际的应用上，BF算法相对于KMP算法来说使用可能更为方便、简洁，实操性更强。但是KMP算法的意义在于，这是人类第一次发现
串的模式匹配问题能够以线性模式来简化。在KMP的学习上，与其说是学会了一种数据结构，不妨说是与自己来了一场头脑风暴。当然，
生命不息，进步不止，在查阅KMP资料的时候，后人对于一开始的版本也进行了更多的优化，不断完善。

             时间复杂度             空间复杂度
BF算法         O(n*m)                O(1)
KMP算法        O(n+m)                O(m)
注：n为主串长度，m为模式串长度。KMP算法牺牲了一定的空间换取时间上的简化。
解析：KMP算法的时间复杂度由匹配的时间复杂度O(n)+求next数组的时间复杂度O(m)求得
     空间复杂度为辅助数组next[m]求得

---

参考资料：

1.百度百科 https://baike.baidu.com/item/kmp%E7%AE%97%E6%B3%95/10951804?fr=aladdin

2.https://blog.csdn.net/x__1998/article/details/79951598

3.《数据结构（c语言版）》李云清等编著

---

以上仅为自己的一些拙见，如有不正确的地方欢迎指出。