Ng第十二课:支持向量机(Support Vector Machines)(三)
11 SMO优化算法(Sequential minimal optimization)
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。关于SMO最好的资料就是他本人写的《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》。
首先回到前面一直悬而未解的问题,对偶函数最后的优化问题:
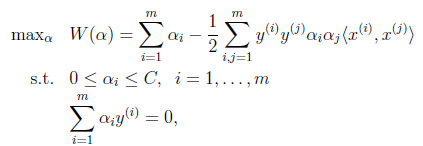
要解决的是在参数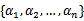 上求最大值W的问题,至于
上求最大值W的问题,至于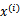 和
和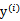 都是已知数。C由我们预先设定,也是已知数。
都是已知数。C由我们预先设定,也是已知数。
按照坐标上升的思路,首先固定除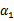 以外的所有参数,然后在
以外的所有参数,然后在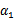 上求极值。等一下,这个思路有问题,因为如果固定
上求极值。等一下,这个思路有问题,因为如果固定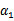 以外的所有参数,那么
以外的所有参数,那么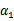 将不再是变量(最大值W确定其他所有值也确定)。因为问题中规定了
将不再是变量(最大值W确定其他所有值也确定)。因为问题中规定了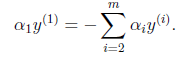 (如果其他值是定量那么a1y(1)出来的结果也是定量)
(如果其他值是定量那么a1y(1)出来的结果也是定量)
因此,需要一次选取两个参数做优化,比如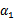 和
和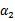 ,此时
,此时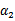 可以由
可以由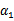 和其他参数表示出来。这样回带到W中,W就只是关于
和其他参数表示出来。这样回带到W中,W就只是关于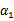 的函数了,可解。
的函数了,可解。
这样,SMO的主要步骤如下:

意思是,第一步选取一对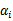 和
和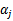 ,选取方法使用启发式方法(后面讲)。第二步,固定除
,选取方法使用启发式方法(后面讲)。第二步,固定除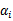 和
和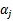 之外的其他参数,确定W极值条件下的
之外的其他参数,确定W极值条件下的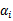 ,
,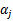 由
由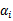 表示。
表示。
SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效。
下面讨论具体方法:
假设我们选取了初始值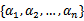 满足了问题中的约束条件(用了启发式方法)。接下来,住固定
满足了问题中的约束条件(用了启发式方法)。接下来,住固定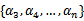 ,这样W就是
,这样W就是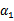 和
和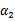 的函数。并且
的函数。并且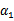 和
和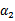 满足条件:
满足条件:
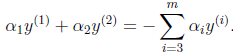
由于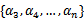 都是已知固定值,因此为了方面,可将等式右边标记成实数值
都是已知固定值,因此为了方面,可将等式右边标记成实数值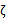 。
。
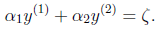
当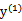 和
和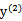 异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
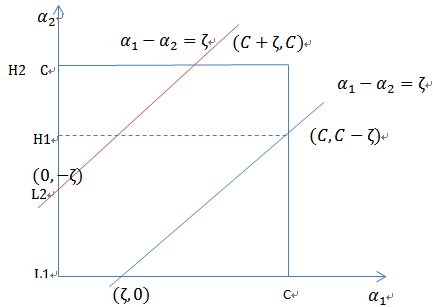
横轴是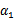 ,纵轴是
,纵轴是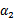 ,
,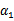 和
和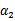 既要在矩形方框内,也要在直线上,因此
既要在矩形方框内,也要在直线上,因此
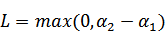 ,
,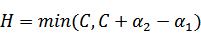
同理,当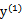 和
和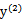 同号时,
同号时,
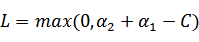 ,
,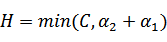
然后将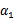 用
用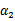 表示:
表示:
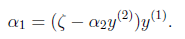
然后反代入W中,得
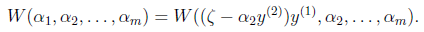
展开后W可以表示成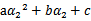 。其中a,b,c是固定值。这样,通过对W进行求导可以得到
。其中a,b,c是固定值。这样,通过对W进行求导可以得到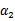 ,然而要保证
,然而要保证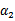 满足
满足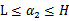 ,我们使用
,我们使用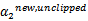 表示求导求出来的
表示求导求出来的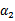 ,然而最后的
,然而最后的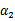 ,要根据下面情况得到:
,要根据下面情况得到:
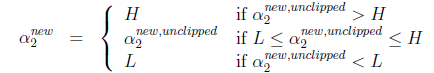
这样得到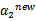 后,我们可以得到
后,我们可以得到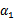 的新值
的新值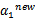 。
。
12 SMO中拉格朗日乘子的启发式选择方法
所谓的启发式选择方法主要思想是每次选择拉格朗日乘子的时候,优先选择样本前面系数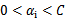 的
的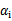 作优化,因为在界上(
作优化,因为在界上(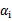 为0或C)的样例对应的系数
为0或C)的样例对应的系数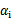 一般不会更改。
一般不会更改。
这条启发式搜索方法是选择第一个拉格朗日乘子用的,比如前面的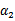 。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个
。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个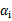 中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表
中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表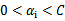 ,在界上也有可能会违背。是的,因此在给定初始值
,在界上也有可能会违背。是的,因此在给定初始值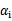 =0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对
=0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对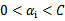 的样例进行迭代更新。
的样例进行迭代更新。
在第一个乘子选择后,第二个乘子也使用启发式方法选择,第二个乘子的迭代步长大致正比于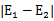 ,选择第二个乘子能够最大化
,选择第二个乘子能够最大化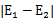 。即当
。即当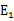 为正时选择负的绝对值最大的
为正时选择负的绝对值最大的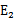 ,反之,选择正值最大的
,反之,选择正值最大的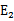 。
。
最后的收敛条件是在界内(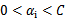 )的样例都能够遵循KKT条件,且其对应的
)的样例都能够遵循KKT条件,且其对应的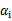 只在极小的范围内变动。
只在极小的范围内变动。
至于如何写具体的程序,请参考John C. Platt在论文中给出的伪代码。
13 总结
其实在应用时不需要这么多推导,直接用结论写程序即可。拉格朗日对偶的重要作用是将w的计算提前并消除w,使得优化函数变为拉格朗日乘子的单一参数优化问题。
对比这么复杂的推导过程,SVM的思想确实那么简单。它不再像logistic回归一样企图去拟合样本点(中间加了一层sigmoid函数变换),而是就在样本中去找分隔线,为了评判哪条分界线更好,引入了几何间隔最大化的目标。
之后所有的推导都是去解决目标函数的最优化上了。在解决最优化的过程中,发现了w可以由特征向量内积来表示,进而发现了核函数,仅需要调整核函数就可以将特征进行低维到高维的变换,在低维上进行计算,实质结果表现在高维上。由于并不是所有的样本都可分,为了保证SVM的通用性,进行了软间隔的处理,导致的结果就是将优化问题变得更加复杂,然而惊奇的是松弛变量没有出现在最后的目标函数中。最后的优化求解问题,也被拉格朗日对偶和SMO算法化解,使SVM趋向于完美。
Ng第十二课:支持向量机(Support Vector Machines)(三)的更多相关文章
- 十二、支持向量机(Support Vector Machines)
12.1 优化目标 参考视频: 12 - 1 - Optimization Objective (15 min).mkv 到目前为止,你已经见过一系列不同的学习算法.在监督学习中,许多学习算法的性能都 ...
- 【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 12—Support Vector Machines 支持向量机
Lecture 12 支持向量机 Support Vector Machines 12.1 优化目标 Optimization Objective 支持向量机(Support Vector Machi ...
- [C7] 支持向量机(Support Vector Machines) (待整理)
支持向量机(Support Vector Machines) 优化目标(Optimization Objective) 到目前为止,你已经见过一系列不同的学习算法.在监督学习中,许多学习算法的性能都非 ...
- 斯坦福第十二课:支持向量机(Support Vector Machines)
12.1 优化目标 12.2 大边界的直观理解 12.3 数学背后的大边界分类(可选) 12.4 核函数 1 12.5 核函数 2 12.6 使用支持向量机 12.1 优化目标 到目前为 ...
- 机器学习课程-第7周-支持向量机(Support Vector Machines)
1. 优化目标 在监督学习中,许多学习算法的性能都非常类似,因此,重要的不是你该选择使用学习算法A还是学习算法B,而更重要的是,应用这些算法时,所创建的大量数据在应用这些算法时,表现情况通常依赖于你的 ...
- Ng第十二课:支持向量机(Support Vector Machines)(一)
1 目录 支持向量机基本上是最好的有监督学习算法了,从logistic回归出发,引出了SVM,揭示模型间的联系,过渡自然. 2 重新审视logistic回归 Logistic回归目的是从特征学习出一个 ...
- Ng第十二课:支持向量机(Support Vector Machines)(二)
7 核函数(Kernels) 最初在“线性回归”中提出的问题,特征是房子的面积x,结果y是房子的价格.假设从样本点的分布中看到x和y符合3次曲线,那么我们希望使用x的三次多项式来逼近这些样本点.那么首 ...
- stanford coursera 机器学习编程作业 exercise 6(支持向量机-support vector machines)
在本练习中,先介绍了SVM的一些基本知识,再使用SVM(支持向量机 )实现一个垃圾邮件分类器. 在开始之前,先简单介绍一下SVM ①从逻辑回归的 cost function 到SVM 的 cost f ...
- 机器学习(八)--------支持向量机 (Support Vector Machines)
与逻辑回归和神经网络相比,支持向量机或者简称 SVM,更为强大. 人们有时将支持向量机看作是大间距分类器. 这是我的支持向量机模型代价函数 这样将得到一个更好的决策边界 理解支持向量机模型的做法,即努 ...
随机推荐
- mysql联表更新使用join
update TableA as a inner join TableB as b on a.order_id=b.order_id set a.last_time='2018-01-01' whe ...
- css背景图充满屏幕
代码: body { /* 加载背景图 */ background: url(resource/inv_bg.png); /* 背景图不平铺 */background-repeat: no-repea ...
- Mybatlis SQL 注入与防范
SQL注射原理 所谓SQL注入,就是通过把SQL命令插入到Web表单提交或输入域名或页面请求的查询字符串,最终达到欺骗服务器执行恶意的SQL命令.具体来说,它是利用现有应用程序,将(恶意)的SQL命令 ...
- 厉害了,PS大神真的能改变世界!
今天要介绍的这位PS大神 名叫 Katrina Yu 她的操作真的神了 不管多普通的场景 她都能帮你改头换面 在后院破旧的椅子上喝着咖啡 一转眼就骑着魔法扫帚 飞上了天,与月亮肩并肩 看原图还以为是在 ...
- Python之路(第二十篇) subprocess模块
一.subprocess模块 subprocess英文意思:子进程 那什么是进程呢? (一)关于进程的相关理论基础知识 进程是对正在运行程序的一个抽象,进程的概念起源于操作系统,是操作系统最核心的概念 ...
- ajax异步请求该嵌套还是并列?
因为要查询两个数据库表才能确定我所需要的数据范围,所以前台js得发两次ajax请求.问题就是,这两个请求是嵌套着写:{发,接{发,接}}:还是并列着写:{发,接},{发,接} 好? 答案:如果2次aj ...
- 拼图类APP原型模板分享——简拼
简拼是一款记录美好.抒写情怀的拼图APP,模板设计风格简约文艺,种类齐全. 此原型模板所用到的组件有标签组.水平分隔线.圆形工具.交互动作有结合标签组实现页面跳转,选择组件触发按钮状态变化等. 此原型 ...
- PDF下载网
http://www.java1234.com/a/javabook/javaweb/2018/1103/12297.html
- 微信小程序获取当前位置
详细参数说明请看小程序api文档:https://developers.weixin.qq.com/miniprogram/dev/api/wx.openLocation.html wx.getLoc ...
- Web Api 2 认证与授权 2
HTTP Message Handler 在 Web Api 2 认证与授权 中讲解了几种实现机制,本篇就详细讲解 Message Handler 的实现方式 关于 Message Handler 在 ...
