【Coursera-ML-Notes】线性回归（上）

什么是机器学习

关于机器学习，有以下两种不同的定义。

机器学习是研究如何使电脑具备学习能力，而不用显式编程告诉它该怎么做。

the field of study that gives computers the ability to learn without being explicitly programmed.​

机器学习能够使电脑程序从以往的经验（E）中学习并改善自己，从而在处理新的任务（T）时提升它的性能（P）。

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

这里针对第二种定义举个例子：下围棋

E：程序模拟人类下很多盘棋所积累的经验

T：下围棋这个任务

P：程序赢得下次比赛的几率

模型表示

假定我们现有一大批数据，包含房屋的面积和对应面积的房价信息，如果我们能得到房屋面积与房屋价格间的关系，那么，给定一个房屋时，我们只要知道其面积，就能大致推测出其价格了。

以这个问题为例，可以建立一个回归模型，首先明确几个常用的数学符号：

• 输入变量：\(x^{(i)}\)，也叫做输入特征，如这个例子中的面积

• 输出变量：\(y^{(i)}\)，也叫做目标变量，如例子中的我们需要预测的房价

• 训练样本：\((x^{(i)},y^{(i)})\)是输入变量和输出变量称为一组训练样本

• 训练集（Training set）：\(i=1,...,m\)，这么多组训练样本构成训练集

• 假设（hypothesis）：也称预测函数，比如例子中可以建立这样一个线性函数：
  \[
  h_θ(x)=θ_0+θ_1x_1
  \]

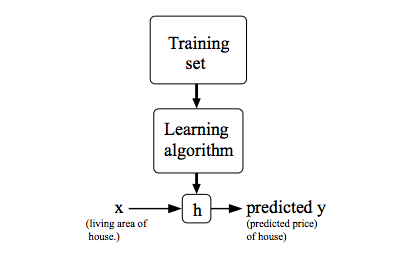
我们的目标是找到满足这样一个线性函数来拟合训练集中的数据，那么，给定一个房屋时，我们只要知道其面积，就能大致推测出其价格了。这个过程可以用下图来表示：

代价函数

有了模型，我们还需要评估模型的准确性。于是代价函数就被引进，它也叫做平方误差函数。
\[
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
\]
可以看出，代价函数是采取预测值和真实值差值的平方和取均值的方式来评估数据的拟合程度的，代价函数的值越小，表示模型对于数据的拟合程度越高。

梯度下降

有了模型和评价模型的方式，现在我们要确定模型中的参数\(\theta_0\)和\(\theta_1\)，以找到最好的模型。

以\(\theta_0\)为\(x\)轴，\(\theta_1\)为\(y\)轴，代价函数\(J(\theta)\)为\(z\)轴，建立三维坐标系，可以得到如下图所示的图像：

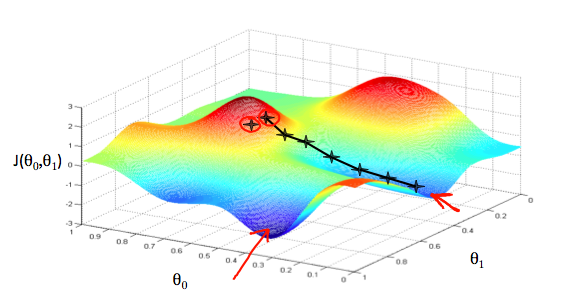
如果把这个图像看作是一座山的话，我们有一个起点\((\theta_0,\theta_1,J(\theta_0,\theta_1))\)，现在要从这个点找到一条最快的路径到达山脚下，数学上来说，梯度是最陡峭的方向，所以我们要始终沿着梯度的方向走。

学习率

方向已经确定，但是往这个方向前进的距离是多少呢？这个距离由学习率\(\alpha\)来确定。有了方向和步距，那么\(\theta_0、\theta_1\)的变化规律如下：

那么怎么样确定学习率\(\alpha\)（步距）呢？

如果步距过大，可能接近收敛的时候会越过收敛点，甚至最终无法收敛。

如果步距过小，收敛所花的时间会很久。

所以我们要调节\(\alpha\)的大小，使收敛时间在一个合理的范围里。

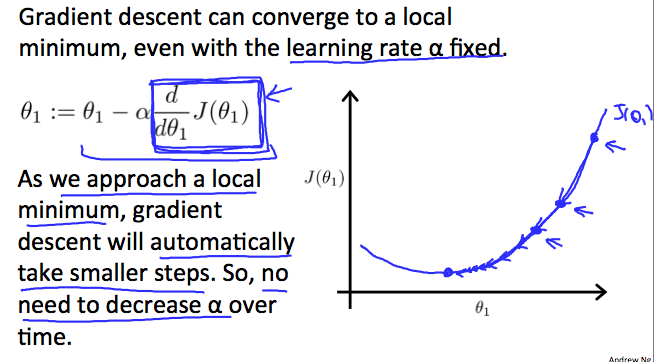
在每一次迭代过程中，需要改变\(\alpha\)的大小吗？如果不需要的话，接近收敛时，会不会因为步距偏大而越过收敛点？

在迭代过程中不需要改变\(\alpha\)的大小，因为接近收敛点时，梯度(斜率)会变小，等价于步距在自动变小，所以没有必要减小\(\alpha\)。

最后，为什么代价函数的表达式中为什么取均值的除数是\(2m\)而不是\(m\)？

我们来看一看参数每一次的迭代过程都发生了什么？
\[
\begin{equation}
θ_0:=θ_0-a\frac{∂}{∂θ_0}J(θ_0,θ_1)
\end{equation}
\]
对上式化简，

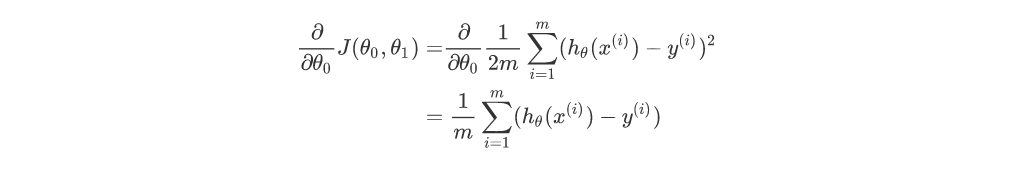
因此，

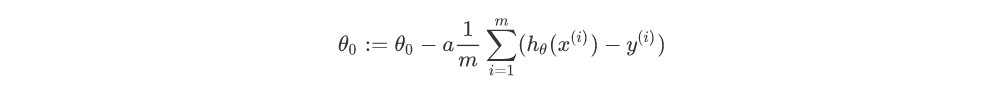
所以取2m的原因其实是为了求导数时化简方便，可以和平方项的2约掉。