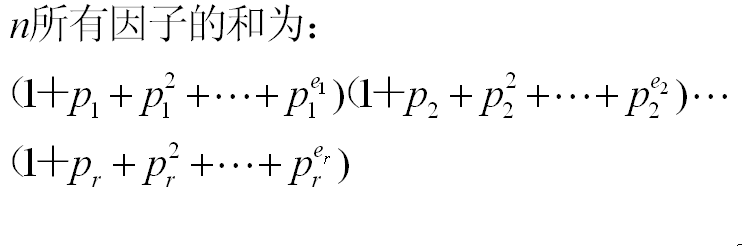求N的因子之和。
理论依据:
代码:
/*
显然,数据够大的时候,数组要用 __int64 */ #include<iostream>
#include<map>
#include<cstdio>
#include<cstdlib>
#include<cstring> using namespace std; bool s[];
int num[];//用来%j
int ans[];//保存和。 void make_ini() //全部扫一遍。筛选一下。
{
int i,j,k,t;
for(i=;i<=;i++)
{
num[i]=i;
ans[i]=;
}
for(i=;i<=;i++)
if(s[i]==false)//是素数
{
for(j=i;j<=;j=j+i)//枚举每个素数的倍数
{
// if(j%i==0) //这个肯定成立,不需要
{
k=;t=;
while(num[j]%i==)
{
num[j]=num[j]/i;
t=t*i;//关键部分。
k=k+t;//关键部分
}
ans[j]=ans[j]*k;
}
s[j]=true;
}
}
} int main()
{
int n;
make_ini();
while(scanf("%d",&n)>)
{
printf("%d\n",ans[n]-n);
}
return ;
}
求N的因子之和。的更多相关文章
- 求n的因子个数与其因子数之和
方法一:朴素算法:O(n). #include<bits/stdc++.h> using namespace std; int get_num(int n){ ; ;i<=n;++i ...
- 72. 求m到n之和
求m到n之和 int sum(int m, int n) { int i, result = 0; for (i=m; i<=n; i++) result = result+i; return ...
- 《剑指offer》写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
弱菜刷题还是刷中文题好了,没必要和英文过不去,现在的重点是基本代码能力的恢复. [题目] 剑指offer 写一个函数,求两个整数之和,要求在函数体内不得使用+.-.*./四则运算符号. [思路] 直觉 ...
- hdu6446 网络赛 Tree and Permutation(树形dp求任意两点距离之和)题解
题意:有一棵n个点的树,点之间用无向边相连.现把这棵树对应一个序列,这个序列任意两点的距离为这两点在树上的距离,显然,这样的序列有n!个,加入这是第i个序列,那么这个序列所提供的贡献值为:第一个点到其 ...
- 求一个整数个位数之和 Exercise06_02
import java.util.Scanner; /** * @author 冰樱梦 * 时间:2018年下半年 * 题目:求一个整数个位数之和 * */ public class Exercise ...
- JAVA 基础编程练习题20 【程序 20 求前 20 项之和】
20 [程序 20 求前 20 项之和] 题目:有一分数序列:2/1,3/2,5/3,8/5,13/8,21/13...求出这个数列的前 20 项之和. 程序分析:请抓住分子与分母的变化规律. pac ...
- 代码实现:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如6=1+2+3.第二个完全数是28, //它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加, //编程找出1000以内的所有完数。
import java.util.ArrayList; import java.util.List; //一个数如果恰好等于它的因子之和,这个数就称为"完数".例如6=1+2+3. ...
- java 求数组最大子序列之和
经典问题: 给定一个int[]数组,求其最大子序列之和(条件:数组中不全部都是负数). 最优算法,线性时间复杂度: public static int maxSubSum(int[] a){ int ...
- python基础练习题(题目 一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如6=1+2+3.编程找出1000以内的所有完数)
day12 --------------------------------------------------------------- 实例019:完数 题目 一个数如果恰好等于它的因子之和,这个 ...
随机推荐
- BZOJ 1002--[FJOI2007]轮状病毒(高精度)
1002: [FJOI2007]轮状病毒 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 6858 Solved: 3745[Submit][Statu ...
- Swift里字符串(五)Native strings
Native strings have tail-allocated storage, which begins at an offset of nativeBias from the storage ...
- iOS-WKWebview 带有进度条加载的ViewController【KVO监听Webview加载进度】
前言 为什么要说 WKWebview,在之前做电子书笔记时已经提过 WKWebview 在iOS8之后已完全替代 Webview,原因就不多说了,主要还是内存过大: 封装 封装一个基于 UIViewC ...
- 【Azure】Publish Error of "%(TargetOSFamily.Identity)" that evaluates to "" instead of a number
在向Azure部署程序的时候,出现如下错误: A numeric comparison was attempted on "%(TargetOSFamily.Identity)" ...
- ContentProvider类的设计分析
ContentProvider的类设计很好,Transport作为成员存在,完成Binder的功能,有点像组合模式,把完成转发/通信功能 封装为一个内部类,便于转发外部调用给外部类,这种设计在Andr ...
- Linux驱动:LCD驱动框架分析
一直想花时间来整理一下Linux内核LCD驱动,却一直都忙着做其他事情去了,这些天特意抽出时间来整理之前落下的笔记,故事就这样开始了.LCD驱动也是字符设备驱动的一种,框架上相对于字符设备驱动稍微复杂 ...
- 杂记---Mongo的Invalid BSON field name $gte
1.前言 这几天使用mongo的时候遇到了一个异常:Invalid BSON field name $gte,该问题可能会有很多小伙伴会遇到,因此记录一下解决过程.起因是用JAVA翻译一个其他语言写的 ...
- Impala配置HA-Nginx
Impala的高可用配置,官方的例子用的是Haproxy,考虑到nginx配置简单,使用人群广泛,再加上nginx1.9以后支持TCP的负载均衡,所以选用nginx. nginx安装:yum inst ...
- 解决LNMP环境下WordPress后台缺少”WP-ADMIN”路径
LNMP一键安装包也是老左比较喜欢使用的环境之一,昨天帮助一个网友搭建LNMP环境后发现登陆WP后台之后点击左侧的菜单发现直接跳转404错误,开始还以为数据库问题,视线朝上一看原来在地址栏中的路径缺少 ...
- Pelican+Github博客搭建详细教程
操作系统:Mac OS / Linux 工具集: 1.Pelican--基于Python的静态网页生成器 2.马克飞象--Evernote出的Markdown文本编辑器 3.GoDaddy--域名供应 ...