CodeForces1006E- Military Problem

E. Military Problem

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In this problem you will have to help Berland army with organizing their command delivery system.

There are nn officers in Berland army. The first officer is the commander of the army, and he does not have any superiors. Every other officer has exactly one direct superior. If officer aa is the direct superior of officer bb, then we also can say that officer bb is a direct subordinate of officer aa.

Officer xx is considered to be a subordinate (direct or indirect) of officer yy if one of the following conditions holds:

• officer yy is the direct superior of officer xx;
• the direct superior of officer xx is a subordinate of officer yy.

For example, on the picture below the subordinates of the officer 33 are: 5,6,7,8,95,6,7,8,9.

The structure of Berland army is organized in such a way that every officer, except for the commander, is a subordinate of the commander of the army.

Formally, let's represent Berland army as a tree consisting of nn vertices, in which vertex uu corresponds to officer uu. The parent of vertex uucorresponds to the direct superior of officer uu. The root (which has index 11) corresponds to the commander of the army.

Berland War Ministry has ordered you to give answers on qq queries, the ii-th query is given as (ui,ki)(ui,ki), where uiui is some officer, and kiki is a positive integer.

To process the ii-th query imagine how a command from uiui spreads to the subordinates of uiui. Typical DFS (depth first search) algorithm is used here.

Suppose the current officer is aa and he spreads a command. Officer aa chooses bb — one of his direct subordinates (i.e. a child in the tree) who has not received this command yet. If there are many such direct subordinates, then aa chooses the one having minimal index. Officer aa gives a command to officer bb. Afterwards, bb uses exactly the same algorithm to spread the command to its subtree. After bb finishes spreading the command, officer aa chooses the next direct subordinate again (using the same strategy). When officer aa cannot choose any direct subordinate who still hasn't received this command, officer aa finishes spreading the command.

Let's look at the following example:

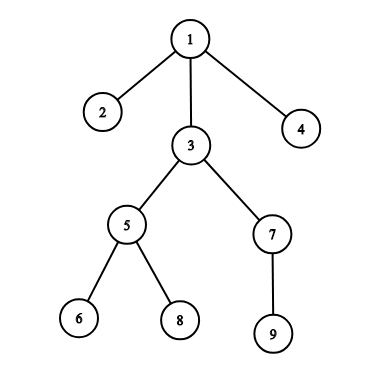
If officer 11 spreads a command, officers receive it in the following order: [1,2,3,5,6,8,7,9,4][1,2,3,5,6,8,7,9,4].

If officer 33 spreads a command, officers receive it in the following order: [3,5,6,8,7,9][3,5,6,8,7,9].

If officer 77 spreads a command, officers receive it in the following order: [7,9][7,9].

If officer 99 spreads a command, officers receive it in the following order: [9][9].

To answer the ii-th query (ui,ki)(ui,ki), construct a sequence which describes the order in which officers will receive the command if the uiui-th officer spreads it. Return the kiki-th element of the constructed list or -1 if there are fewer than kiki elements in it.

You should process queries independently. A query doesn't affect the following queries.

Input

The first line of the input contains two integers nn and qq (2≤n≤2⋅105,1≤q≤2⋅1052≤n≤2⋅105,1≤q≤2⋅105) — the number of officers in Berland army and the number of queries.

The second line of the input contains n−1n−1 integers p2,p3,…,pnp2,p3,…,pn (1≤pi<i1≤pi<i), where pipi is the index of the direct superior of the officer having the index ii. The commander has index 11 and doesn't have any superiors.

The next qq lines describe the queries. The ii-th query is given as a pair (ui,kiui,ki) (1≤ui,ki≤n1≤ui,ki≤n), where uiui is the index of the officer which starts spreading a command, and kiki is the index of the required officer in the command spreading sequence.

Output

Print qq numbers, where the ii-th number is the officer at the position kiki in the list which describes the order in which officers will receive the command if it starts spreading from officer uiui. Print "-1" if the number of officers which receive the command is less than kiki.

You should process queries independently. They do not affect each other.

Example

input

Copy

9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9

output

Copy

3
6
8
-1
9
4

题解：记录每个节点的时间戳和其有几个子节点即可；DFS

AC代码为：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
int n, m, a, b, c = 1, d;
bool vis[maxn] = { false };
vector<int> graph[maxn];
int level[maxn],pos[maxn],child[maxn];
int dfs(int src) 
{
    vis[src] = true;
    pos[c] = src;
    level[src] = c++;
    int temp = 1;
    for (int i = 0; i<graph[src].size(); i++) 
    {
        if (!vis[graph[src][i]]) temp += dfs(graph[src][i]);
    }
    return  child[src] = temp;
}
int main() 
{
    cin >> n >> m;
    for (int i = 2; i <= n; i++) 
    {
        cin >> a;
        graph[a].push_back(i);
    }
    dfs(1);
    while (m--) 
    {
        cin >> a >> b;
        if (child[a]<b) cout << -1 << endl;
        else cout << pos[level[a] + b - 1] << endl;
    }
    return 0;
}