深度优先搜索 & 广度优先搜索

目录

• 邻接表
  • 邻接表的深度优先搜索
  • 邻接表的广度优先搜索
• 临接数组
  • 临接数组的深度优先搜索
  • 临接数组的广度优先搜索
• 二叉树
  • 二叉树的深度优先搜索
  • 二叉树的广度优先搜索

邻接表

邻接表的深度优先搜索

假如我们有如下无向图

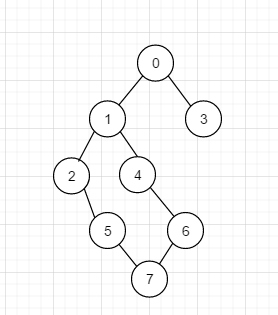
如果我们想对其进行深度优先遍历的话, 其实情况不止一种, 比如 0 1 2 5 7 6 4 3

下面介绍使用临接表法对其进行遍历, 一般邻接表长下面这样:

**思路: ** 参照上下两图我们可以发现, 邻接表中的左半部分是一个链表数组, 0-6 一共7个位置, 每一个位置上都对应一个链表, 比如 下面的 位置0 , 表示它是第一个节点, 右边的链表中的node1 和 node3 分别表示他们的位置0处节点的相邻节点,

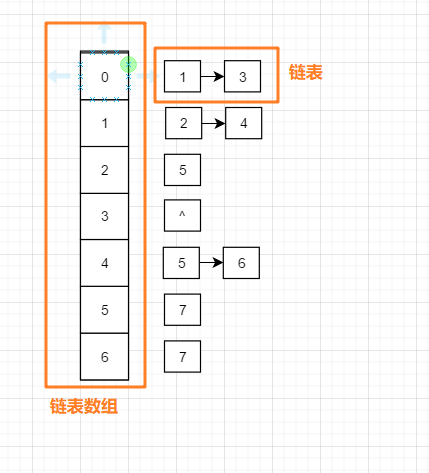
深度优先就是一条路走到黑, 走不下去了就往回退, 所以通常使用递归;

思路:

比如我们从node0开始, 然后可以往node1 也可以往node3 , 随便选一个 node1 , 再从node1开始往下走, 我们可以到node2 或者 node4 --- 这种走法结合上图来看, 翻译一下就是下面这样

1. 打印当前节点值
2. 标记当前节点被访问过
3. 遍历当前节点的邻接表
   1. 如果邻接表中的元素曾经被访问过, 跳过
   2. 如果邻接表中的节点未被访问过, 就 重复123过程

封装邻接表

public class Graph {
    private int size;
    // 链表数组实现邻接表
    private LinkedList<Integer> list[];

    public Graph(int size) {
        this.size = size;
        list = new LinkedList[size];
        for (int i = 0; i < size; i++) {
            list[i] = new LinkedList<>();
        }
    }

    /**
     * 接收两个顶点 , 添加边
     *
     * @param a
     * @param b
     */
    public void addEdge(int a, int b) {
        list[a].add(b);
        list[b].add(a);
    }

      public static void main(String[] args) {
        Graph graph = new Graph(8);
        graph.addEdge(0, 1);
        graph.addEdge(0, 3);
        graph.addEdge(1, 2);
        graph.addEdge(1, 4);
        graph.addEdge(2, 5);
        graph.addEdge(4, 5);
        graph.addEdge(4, 6);
        graph.addEdge(5, 7);
        graph.addEdge(6, 7);

        graph.dfs(0);
      }
}

深度优先遍历

    public void dfs(int start) {
        boolean[] visited = new boolean[this.size];
        dodfs(start, this.list, visited);
    }

    /**
     * 递归深度搜索
     *
     * @param list
     * @param visited
     */
    private void dodfs(int start, LinkedList<Integer>[] list, boolean[] visited) {
        // 检查当前节点有没有被访问过
        if (visited[start]) {
            return;
        }
        System.out.println(start);
        visited[start] = true;
        for (int i = 0; i < this.list[start].size(); i++) {
            int node = this.list[start].get(i);
            dodfs(node, list, visited);
        }
    }

邻接表的广度优先搜索

还是看这个图, 广度优先遍历的话,就是按层遍历 , 比如 0 1 3 2 4 5 6 7

其实这样的话再不能使用递归设计函数了, 其实我当时应该能判断出来, 递归的话容易往图的一边跑, 一边遍历完事后才可能进行另一面的遍历, 可惜了,被问蒙了...

广度优先的思路:

使用一个队列来辅助完成, 思路如下

1. 将当前节点添加进队列
2. 打印当前节点的值
3. 遍历当前节点的邻接表中的节点
   1. 如果节点曾经被访问过, 跳过,不处理他
   2. 如果当前节点没有被访问过, 并且队列中现在没有这个节点, 就将它添加进队列
4. 移除并得到 头节点
5. 将头结点在辅助数组visited中的标记 置为 true , 标识这个节点被访问过了
6. 更新位置标记, 什么标记呢? 就是当前队列头位置的node , 在邻接表中的位置

代码如下:

 /**
     * 广度优先搜索
     *
     * @param start
     */
    public void bfs(int start) {
        boolean[] visited = new boolean[this.size];
        dobfs(start, visited, this.list);

    }

    /**
     * 广度优先搜索
     *
     * @param start
     * @param visited
     * @param list
     */
    private void dobfs(int start, boolean[] visited, LinkedList<Integer>[] list) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(start);
        while (queue.size() > 0) {
            // 打印当前的节点
            System.out.println(queue.peek());
            for (int i = 0; i < this.list[start].size(); i++) {
                if (visited[this.list[start].get(i)]) {
                    continue;
                }
                /**
                 *  解决下面情况
                 *     1
                 *    / \
                 *   2   3
                 *    \ /
                 *     5
                 */
                if (!queue.contains(this.list[start].get(i))){
                    queue.add(this.list[start].get(i));
                }
            }

            // 移除头结点
            Integer poll = queue.poll();
            visited[poll] = true;
            // 更新start值
            if (queue.size() > 0) {
                start = queue.peek();
            }
        }
    }

临接数组

临接数组的深度优先搜索

**什么是临接数组? **

如下图:

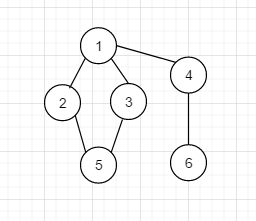
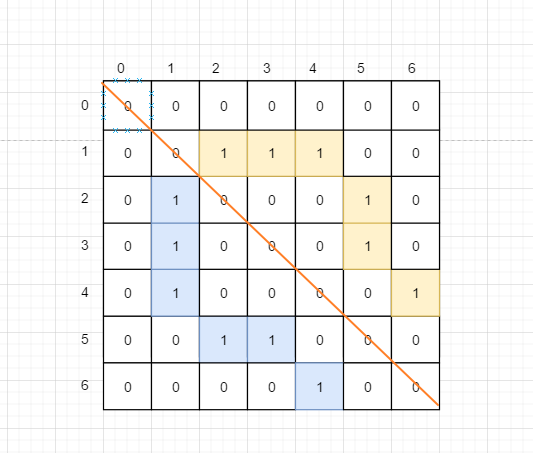
转换成临接矩阵长下面这样, 很清晰的可以看出, 左下角和右上角是对称的, 怎么解读下面的图形呢?

它其实就是一个二维数组 int [权重][X] 二维数组可以理解成数组嵌套数组, 因此前面的 X 其实对应的下图中的一行, 即 一个小数组

• 最左边的 纵向坐标是 0 1 2 3 分别表示当前节点的 权值
• 下图中的每一行都代表着前面的权值对应的 临接点的数量
• 0 表示不是它的临接点 , 1 表示是临接点

创建邻接表的代码如下

public class Graph1 {
    //顶点数
    private int numVertexes;
    // 边数
    private int numEdges;
    // 记录顶点
    int[] vertexes;
    // 二维数组图
    private int[][] points;
    // 用于标记某个点是否被访问过的 辅助数组
    private boolean[] visited;

    private Scanner scanner = new Scanner(System.in);

    public Graph1(int numVertexes, int numEdges) {
        this.numEdges = numEdges;
        this.numVertexes = numVertexes;
        // 初始化邻接矩阵
        this.points = new int[numVertexes][numVertexes];
        // 初始化存放顶点的数组
        this.vertexes = new int[numVertexes];
        // 标记已经访问过的数组
        this.visited = new boolean[this.numVertexes];
    }

    // 构建无向图
    public int[][] buildGraph() {
        System.out.println("请输入顶点的个数");

        this.numVertexes = scanner.nextInt();
        System.out.println("请输入边数");
        this.numEdges = scanner.nextInt();
        // 构建临接矩阵
        for (int i = 0; i < this.numEdges; i++) {
            System.out.println("请输入点(i,j)的 i 值");
            int i1 = scanner.nextInt();
            System.out.println("请输入点(i,j)的 j 值");
            int j1 = scanner.nextInt();
            this.points[i1][j1] = 1;
            this.points[j1][i1] = 1;
        }
        return this.points;
    }

深度优先搜索

思路: 深度优先依然使用递归算法

1. 打印当前节点的值
2. 标记当前节点已经被访问过了
3. 遍历当前节点的临接矩阵
   1. 如果发现遍历的节点为0 , 不处理, 继续遍历
   2. 如果发现遍历的节点为1 , 但是已经被标记访问过了, 不处理, 继续遍历
   3. 如果发现节点值为1 , 且没有被访问过, 递归重复123步骤

  /**
     * 深度搜索
     *
     * @param arr   待搜索的数组
     * @param value 顶点上的值
     */
    public void dfs(int[][] arr, int value) {
        System.out.println(value);
        visited[value] = true;
        for (int i = 0; i < arr.length; i++) {
            if (arr[value][i] != 0 && !visited[i]) {
                dfs(arr, i);
            }
        }
    }

临接数组的广度优先搜索

思路: 广度优先遍历临接矩阵和上面说的邻接表大致相同, 同样需要一个辅助队列

1. 将头结点添加到队列中
2. 打印头结点的值
3. 遍历头结点的临接矩阵
   1. 如果发现遍历的节点为0 , 不处理, 继续遍历
   2. 如果发现遍历的节点为1 , 但是已经被标记访问过了, 不处理, 继续遍历
   3. 如果发现节点值为1 , 且没有被访问过, 且队列中没有这个值 , 重复 123步骤

    /***
     * 广度优先遍历
     *
     * @param arr
     * @param headValue
     */
    public void bfs(int[][] arr, int headValue) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(headValue);
        while (queue.size() > 0) {
            System.out.println(queue.peek());
            for (int i = 0; i < arr[headValue].length; i++) {
                if (arr[headValue][i] == 1&&!visited[i]&&!queue.contains(i)) {
                    queue.add(i);
                }
            }
            // 头节点出队
            Integer poll = queue.poll();
            visited[poll]=true;
            // 更新headValue;
            if (queue.size()>0){
                headValue=queue.peek();
            }
        }
    }

二叉树

假设我们有下面这个二叉树,

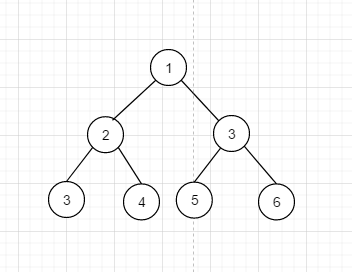
下面我们使用不同的方式遍历它, 如果是深度优先的话, 情况依然是不确定的, 只要是符合一条路走到头, 没路可走再回退就ok , 比如 1 3 6 5 2 3 4

二叉树的深度优先搜索

下面使用java提供的栈这个数据结构辅助完成遍历的过程

**思路: **

1. 将头节点压入栈
2. 弹出栈顶的元素
3. 打印弹出的栈顶的元素的值
4. 处理栈顶元素的子节点
   1. 如果存在左子节点, 将做子节点压入栈
   2. 如果存在右子节点, 将右子节点压入栈
5. 重复 2 3 4 过程...

   /**
     * 深度优先搜索
     * @param node
     */
    private static void dfs( Node node) {
        Stack<Node> stack = new Stack();
        stack.push(node);
        while (!stack.isEmpty()) {
            Node pop = stack.pop();
            System.out.println(pop.getValue());
            if (pop.getLeftNode()!=null){
                stack.push(pop.getLeftNode());
            }
            if (pop.getRightNode()!=null){
                stack.push(pop.getRightNode());
            }
        }
    }

二叉树的广度优先搜索

思路: 广度优先遍历 同样是借助于辅助队列

1. 将顶点添加进队列
2. 打印这个节点的值
3. 处理当前这个压入栈的左右子节点
   1. 如果存在左节点, 将左节点存入队列
   2. 如果存在右节点, 将右节点存入队列
4. 将头结点出队
5. 重复 2 3 4过程

    /**
     * 广度优先搜索
     * @param node
     */
    private static void bfs( Node node) {
        Queue<Node> queue  = new LinkedList<>();
        queue.add(node);
        while (queue.size()>0){
            System.out.println(queue.peek().getValue());
            // 将左右节点入队
            if (queue.size()>0){
                Node nd = queue.poll();
                if (nd.getLeftNode()!=null){
                    queue.add(nd.getLeftNode());
                }
                if (nd.getRightNode()!=null){
                    queue.add(nd.getRightNode());
                }
            }
        }
    }