题解 yzoj1663: 愤怒的牛(二分) yzoj1662: 曲线(三分)

话说二分和三分的题还没有整理过，就趁这两题来整理下笔记

先讲讲关于二分，对于二分的具体边界长期以来对我来说都是个玄学问题，都是边调边拍改对的。思路大体是确定左边界l，和有边界r，判断满足条件缩小范围。

放个大概的代码

while(l+ep<r){
	  lm=l+(r-l)/3.0;
	  rm=r-(r-l)/3.0;
	  if(clu(lm)>clu(rm)) l=lm;
	  else r=rm;
}

二分用处很大，一般用在二分答案以及二分查找，一般看到最大的最小或最小的最大都是二分答案或二分查找题，一般来说二分答案题的套路都大体一致。

二分答案:luogu P1182,P2678

二分查找:luogu P1496(离散化+二分查找)

关于三分，大概就是在二分的基础上，对左右区间再进行一次二分，三分查找一般用来确定单峰函数的最值

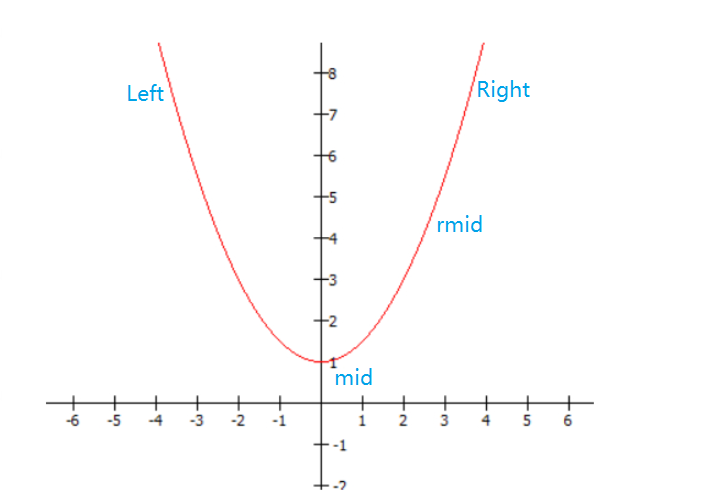
于二分类似先取中间值

mid=(l+r)>>1

再取mid于Right的中间值

rmid=(mid+r)>>1

通过f(mid)于f(rmid)的值来缩小范围

当然还有另外一种写法

1.先把整个区间的n/3的值lmid←n/3+left。

2.再取右侧区间的中间值rmid←right-n/3，从而把区间分为三个小区间。

3.用f(lmid)的值与f(rmid)的值来缩小范围

   double ep=1e-9;
   while(l+ep<r){//使用ep来控制精度
	  lm=l+(r-l)/3.0;
	  rm=r-(r-l)/3.0;
	  if(clu(lm)>clu(rm)) l=lm;
	  else r=rm;
   }

这样的时间复杂度是O(lon3n)

回到题目

1.愤怒的牛

题意:将c头牛放入相隔距离不同的n个牛舍中,要求任意两头牛相隔最小距离最大

对于这道题，我们可以二分查找，注意细节即可

#include<bits/stdc++.h>
using namespace std;
int n,l,r,c,a[100010];
int main(){
	scanf("%d %d",&n,&c);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	sort(a+1,a+1+n);
	l=0,r=a[n];
	while(l<=r){
		int mid=(l+r)>>1;
		int cnt=1;//初始值为1,把第一头牛放到一号牛舍一定最优
		int tmp=a[1];
		for(int i=1;i<=n;++i){
			if(a[i]-tmp>=mid){
				cnt++;
				tmp=a[i];
			}
		}
		if(cnt<c) r=mid-1;
		else l=mid+1;
	}
	printf("%d",r);
	return 0;
}

2.曲线

题意：n个二次函数,第i个二次函数g(x)=aix^2+bix+ci( \(i \epsilon [1, n]\) )(二次函数可能退化为一次函数),f(x)=max(g(x))(n个二次函数中的最大值)

求f(x)在 \(x \epsilon [0, 1000]\) 的最小值,易证f(x)为单峰函数，三分查找即可

#include<bits/stdc++.h>
using namespace std;
int T,n;
double ep=1e-9;//控制精度
double a[10010],b[10010],c[10010];
double clu(double x){
    double sum=0;
    for(int i=1;i<=n;++i) sum=max(sum,((a[i]*x)+b[i])*x+c[i]);//展开即为g(x)
    return sum;
}
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i=1;i<=n;++i){
            scanf("%lf %lf %lf",&a[i],&b[i],&c[i]);
        }
        double l=0,r=1000,lm=0,rm=0;
        while(l+ep<r){
            lm=l+(r-l)/3.0;
            rm=r-(r-l)/3.0;
            if(clu(lm)>clu(rm)) l=lm;
            else r=rm;
        }
        printf("%.4lf\n",clu(l));
    }
    return 0;
}