洛谷P2260 [清华集训2012]模积和（容斥+数论分块）

题意

https://www.luogu.com.cn/problem/P2260

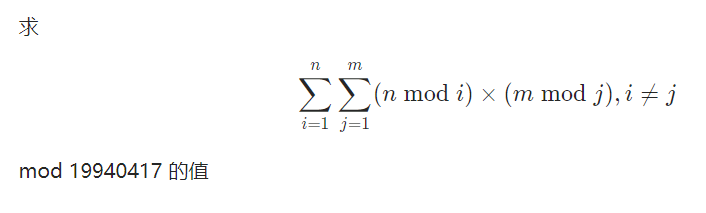
思路

具体思路见下图：

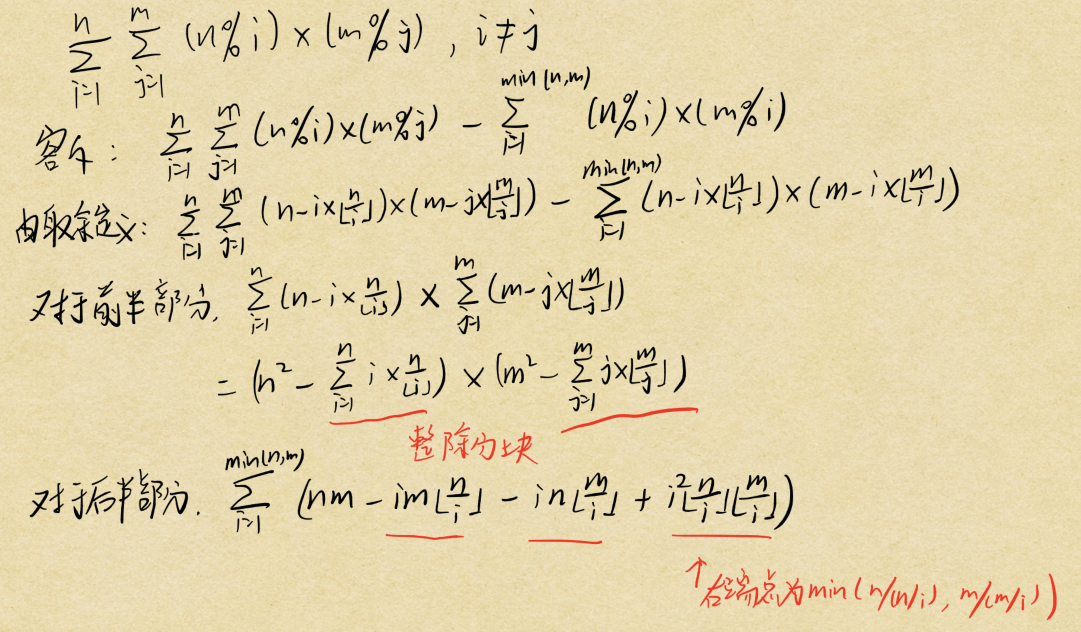
注意这个模数不是质数，不能用快速幂来求逆元，要用扩展gcd。

代码

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=200005;
const int mod=19940417;
const double eps=1e-8;
const double PI = acos(-1.0);
#define lowbit(x) (x&(-x))
ll inv2,inv6,y;
void exgcd(ll a, ll b, ll& x, ll& y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b, y, x);
    y -= a / b * x;
}
ll s(ll x)
{
    return x%mod*(x+1)%mod*(2*x+1)%mod*inv6%mod;
}
ll f(ll x,ll mx)
{
    ll l,r,ans=0;
    for(l=1; l<=mx; l=r+1)
    {
        r=min(mx,x/(x/l));
        ans=(ans+(l+r)%mod*(r-l+1)%mod*inv2%mod*(x/l)%mod)%mod;
    }
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    exgcd(6,mod,inv6,y);
    inv6=(inv6+mod)%mod;
    exgcd(2,mod,inv2,y);
    inv2=(inv2+mod)%mod;
    ll n,m;
    cin>>n>>m;
    ll ans=(n%mod*n%mod-f(n,n)%mod+mod)%mod*(m%mod*m%mod-f(m,m)%mod+mod)%mod;
    ll mn=min(n,m);
    ans=(ans-m%mod*n%mod*mn%mod+mod+f(n,mn)%mod*m%mod+f(m,mn)%mod*n%mod)%mod;
    ll l,r;
    for(l=1; l<=mn; l=r+1)
    {
        r=min(m/(m/l),n/(n/l));
        ans=(ans-(n/l)%mod*(m/l)%mod*(s(r)-s(l-1)%mod)%mod+mod)%mod;
    }
    cout<<ans<<endl;
    return 0;
}