【GCN】图卷积网络初探——基于图（Graph）的傅里叶变换和卷积

2018年11月29日 11:50:38 夏至夏至520 阅读数 5980更多

分类专栏： # MachineLearning

本文链接：https://blog.csdn.net/qq_41727666/article/details/84622965

本文为从CNN到GCN的联系与区别——GCN从入门到精（fang）通（qi）的阅读笔记，文中绝大部分公式和图片摘自原文。
文章目录

一、CNN（卷积神经网络）中的离散卷积

推荐阅读：如何通俗易懂地解释卷积？

1、CNN中的离散卷积：共享参数的过滤器

2、CNN中的卷积操作：通过计算中心像素点以及相邻像素点的【加权和】构成【feature map】;
加权系数=卷积核的权重系数

【实例】下式是一个隐藏神经元的输出计算公式，b为偏置，w为5×5的权重向量，a为上一层的激活值，σ()为激活函数。
可以看出，将上一层的5×5=25的神经元（a）加权（w）求和

3、CNN中的卷积目的：空间特征的提取

4、确定卷积核的系数：随机化初值，训练中根据误差函数loss，通过反向传播+梯度下降进行迭代优化。

二、GCN基本概念介绍

（一）图Graph

定义：顶点和边建立的关系拓扑图

（二）研究GCN的原因

1、CNN的【平移不变性】在【非矩阵结构】数据上不适用

2、希望在【拓扑图】上提取空间特征来进行机器学习

3、GCN主要工作：引入可以优化的【卷积参数】

（三）提取【拓扑图】空间特征的两种方式

1、vertex domain(spatial domain)：顶点域（空间域）

操作：把每个顶点相邻的neighbors找出来

缺点：每个顶点的neighbors不同，计算处理必须针对每个节点

2、spectral domain：谱域

过程：

（1）定义graph上的Fourier Transformation傅里叶变换

（利用Spectral graph theory，借助图的拉普拉斯矩阵的特征值和特征向量研究图的性质）

（2）定义graph上的convolution卷积

三、图的拉普拉斯矩阵

（一）定义：拉普拉斯矩阵L

L=D−AL=D-AL=D−A
其中，L为Laplacian矩阵；
D是顶点的度矩阵（对角矩阵），对角线上的元素依次为各个顶点的度（与该顶点相连的边的条数）；
A是图的邻接矩阵。

计算方法实例：

（二）拉普拉斯矩阵L的良好性质

1、是对称矩阵，可以进行谱分解（特征分解），与GCN的spectral domain对应

2、只在【中心节点】和【一阶相连的顶点】这两种位置上有非0元素，其余位置都是0
注：一阶相连就是通过一条边直接相连，如上图中与顶点1一阶相连的顶点为5和2；
二阶相连就是通过两条边相连，如上图中与顶点1二阶相连的顶点为4（1-5-4）、2（1-5-2）、5（1-2-5）、3（1-2-3）

3、可以通过拉普拉斯算子与拉普拉斯矩阵进行类比

（三）拉普拉斯矩阵L的谱分解（特征分解）

1、矩阵L的特征分解定义：将矩阵L分解为由特征值λ和特征向量u表示的矩阵之积

（1）求特征值和特征向量：λ为特征值，u为特征向量，则满足下式：
Lu=λuLu=\lambda uLu=λu

（2）求特征分解：

令 L是一个 N×N 的方阵，且有 N 个线性无关的特征向量。
这样， L可以被分解为：
L=UΛU−1=U⎛⎝⎜λ1...λ3⎞⎠⎟U−1L=U\Lambda U^{-1} =U\begin{pmatrix}\lambda_1& & \\ &...& \\ & & \lambda_3 \end{pmatrix} U^{-1}L=UΛU−1=U⎝⎛λ1...λ3⎠⎞U−1
其中，U是N×N方阵，且其第i列为L的特征向量ui，ui为列向量；
U=(u1⃗ ,u2⃗ ,...,un⃗ )U=(\vec{u_1},\vec{u_2},...,\vec{u_n})U=(u1,u2,...,un)
Λ是对角矩阵，其对角线上的元素为对应的特征值。

2、拉普拉斯矩阵：【半正定】【对称】矩阵
性质：
（1）有n个线性无关的特征向量
（2）特征值非负
（3）特征向量相互正交，即Q为正交矩阵
设拉普拉斯矩阵L中，λi为特征值，ui为特征向量，U为特征向量ui作为列向量组成的方阵，那么拉普拉斯矩阵的谱分解形式为：

四、Graph上的傅里叶变换与卷积

（一）核心工作

把拉普拉斯算子的【特征函数】
变为
Graph对应的拉普拉斯矩阵的【特征向量】

（二）Graph上的傅里叶变换

1、传统傅里叶变换：

2、Graph上的傅里叶变换

拉普拉斯矩阵=离散拉普拉斯算子
拉普拉斯矩阵的【特征向量U】=拉普拉斯算子的【特征函数exp(-iwt)】

仿照上面传统傅里叶定义，得到Graph上的傅里叶变换：

i为第i个顶点
λl为第l个特征值；ul为第l个特征向量
f为待变换函数，f尖为其对应的傅里叶变换，f和f尖与顶点i一一对应

3、Graph上的傅里叶逆变换：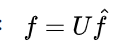

（三）Graph上的卷积

1、传统卷积定理：

f为待卷积函数，h为卷积核（根据需要设计）
f*h为卷积结果

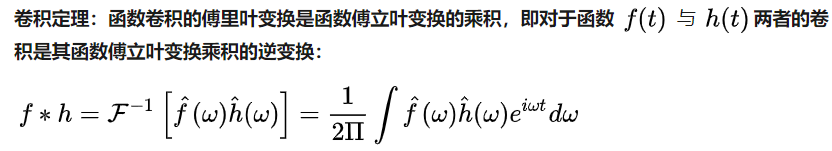
2、Graph上的卷积：仿照上面定义

f为待卷积函数，h为卷积核（根据需要设计）
f*h为卷积结果

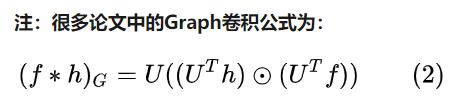
3、由式（1）可以看出，U为特征向量，f为待卷积函数，重点在于设计含有【可训练】【共享参数】的【卷积核h】
卷积参数就是diag(hˆ(λl))卷积参数就是diag(\hat{h}(\lambda_l))卷积参数就是diag(h^(λl))

五、深度学习中的GCN

1、第一代GCN：

卷积核：
diag(hˆ(λl))：diag(θl)diag(\hat{h}(\lambda_l))： diag(\theta_l)diag(h^(λl))：diag(θl)
output公式：
缺点：有n个参数θn，计算量大

2、第二代GCN：

卷积核：
hˆ(λl)：∑Kj=0αjλjl\hat{h}(\lambda_l)：\sum_{j=0}^K \alpha_j\lambda_l^jh^(λl)：j=0∑Kαjλlj
output公式：

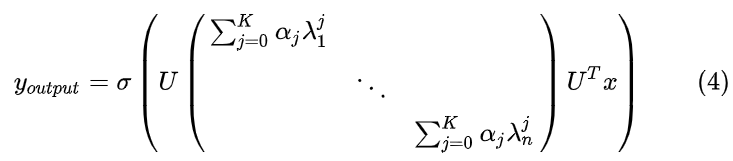
注意到下式：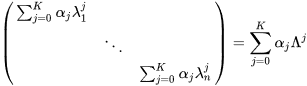

进而可以导出下式：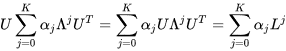

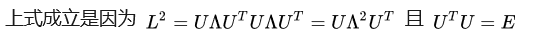
经过矩阵变换，简化后的output公式：

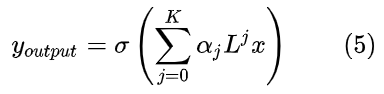
3、实例

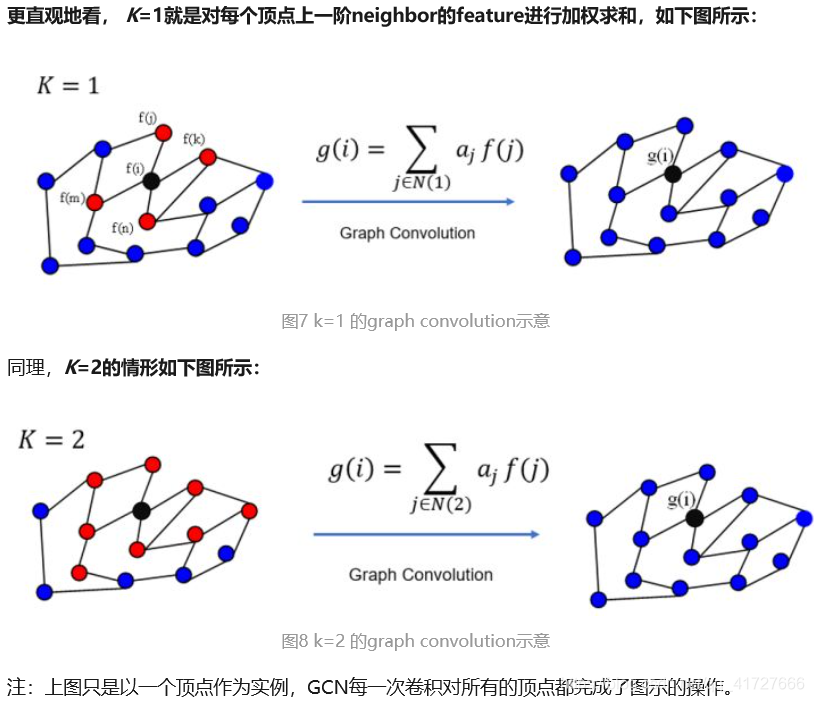
K=1时，对于顶点i，将顶点i以及顶点i的一阶相连顶点（j，k，m，n）的feature值（f函数值）做加权求和，权重就是参数αj，最终输出新的feature值（g函数），为提取得到的空间特征
K=2时，对于顶点i，将顶点i以及顶点i的一阶相连顶点、二阶相连顶点的feature值加权求和，输出新的feature值