最长回文 HDU - 3068（马拉车算法）

Problem Description

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度. 
回文就是正反读都是一样的字符串,如aba, abba等

Input

输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S 
两组case之间由空行隔开(该空行不用处理) 
字符串长度len <= 110000

Output

每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.

Sample Input

aaaa

abab

Sample Output

4
3

先看代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define maxx 101000
char s[maxx],s1[maxx*];
int mp[maxx*];
void Manacher(int l)
{
    int k=;
    s1[k++]='$';s1[k++]='#';
    for(int i=;i<l;i++)
    {
        s1[k++]=s[i];
        s1[k++]='#';
    }
    s1[k]=;
    int mx=,id=;
    for(int i=;i<k;i++)
    {
        mp[i]=mx>i?min(mp[*id-i],mx-i):;
        while(s1[i+mp[i]]==s1[i-mp[i]])
            mp[i]++;
         if(i+mp[i]>mx)
         {
             mx=i+mp[i];
             id=i;
         }
    }
}
int main()
{
    while(~scanf("%s",s))
    {
        int l=strlen(s);
       int ans=;
        Manacher(l);
        for(int i=;i<*l+;i++)
            ans=max(ans,mp[i]-);
        cout<<ans<<endl;
    }
    return ;
}

思路：

代码虽不长，主要需要理解的就是:

mp[i]=mx>i?min(mp[2*id-i],mx-i):1;

一般想法都是从1开始慢慢向两边移动来试探，而马拉车主要就是优化了每次试探P[i]的时候不一定需要从1开始，P[i]代表当前下标i为中心的字符串的回文串半径。

下图中 j 点代表是 i 关于 id 的对称点 ,j=2*id-i;

mx的对称点            j                 id                   i                 mx

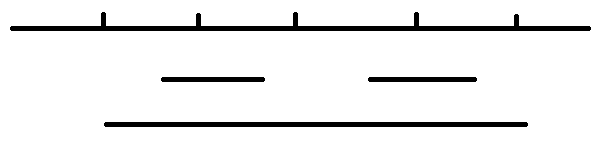
id表示的就是最长回文串的中心，从图观察i与j关于Id对称，i是从2开始枚举过来已经经过了j的位置，那么j位置的最长回文串就可以确定了，如图所示；如果回文串完全被id的回文串所包围，那么根据对称原理i点的回文串的长度最少就是j点回文串的长度。即如果回文串的子串也是回文串，那么这个子串关于主串中心对称而得的子串也是一个回文串。接下来要确定的就是通过j点所能确定的i点回文串的长度最多是多少。首先应该明确，如果i点跑到mx（id点回文串所确定的范围边界）外面去了，那么j点无论如何缩减范围都不可能是id回文串的子串，就不满足上面加粗的结论了。就一定只能从1开始慢慢试探。这就是当mx  < i的时候，MP[i] = 1的原因了。

还有两种情况

一种就是上图中，j所确定的回文串完全被包含，即整个串都是其子串。那么i的可确定回文串范围就是j的回文串范围，MP[i]就变成了MP[j]。

还有一种情况就是j的回文串已经超出了mx的范围

mx的对称点            j                 id                     i              mx

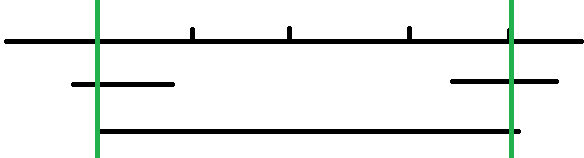
对于绿线以外的区域完全未知，所以必须将MP[j]减去红线外的范围才是i的可确定范围。或者理解为只有两端都去掉外面的部分之后，剩下的才是id回文串的子串，才可以对称过去成为i的回文串。然后再在已确定的范围基础上向两边扩展。