2019牛客多校赛第一场 补题 I题

I题  Points Division

题意：

给你n个点，每个点有坐标(xi,yi)和属性（ai,bi)，将点集划分为两个集合，

任意 A 集合的点 i 和 B 集合点 j, 不允许 xi >= xj 且 yi <= yj。

A 集合的点使用权值 ai，B 集合的点使用权值 bi​，求：

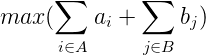
思路：

可以用一条自底向上的折线将这些点分为两组，折线左上为A集合，右下B集合，折线上的点也属于B集合

dp[i] 代表 当前点i在折线上时权值和的最大值

那么对于当前点i来说：

i点之前，y坐标小于yi的点的dp[i]都要加上权值ai (因为当那些点为折线上的点时，当前点i就会被归为A集合）

y坐标大于yi的点的dp[i]都要加上权值bi(因为当那些点为折线上的点时，当前点i会被归为B集合)

计算当前点的dp[i]，因为折线时自底向上的，那么肯定是由当前点下面的点中权值和最大的点max(dp[j])转折的，那么dp[i] = max(dp[j] + bi;

最后取权值和最大

推到这里可以发现需要区间更新，区间最值，单点更新，那么可以直接用线段树来维护。

注意要多加个高度为0的点为折线起始点，这样第一个点就有参照点了，否则无法统计第一个点在折线上和折线下情况的贡献。

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mid ll m = (l + r) >> 1

const int M = 1e5+;
ll mx[M<<],lazy[M<<];
void up(ll rt){
    mx[rt] = max(mx[rt<<],mx[rt<<|]);
}

void pushdown(ll rt){
    if(lazy[rt]){
        lazy[rt<<] += lazy[rt];
        lazy[rt<<|] += lazy[rt];
        mx[rt<<] += lazy[rt];
        mx[rt<<|] += lazy[rt];
        lazy[rt] = ;
    }
}

void build(ll l,ll r,ll rt){
    lazy[rt] = ; mx[rt] = ;
    if(l == r){
        return ;
    }
    mid;
    build(lson); build(rson);
}

void update(ll p,ll c,ll l,ll r,ll rt){
    if(l == r){
        mx[rt] = max(mx[rt],c);
        return ;
    }
    pushdown(rt);
    mid;
    if(p <= m) update(p,c,lson);
    else update(p,c,rson);
    up(rt);
}

void update1(ll L,ll R,ll c,ll l,ll r,ll rt){
    if(L > R) return ;  //会出现L > R的情况，需要判下
    if(L <= l&&R >= r){
        mx[rt] += c;
        lazy[rt] += c;
        return ;
    }
    pushdown(rt);
    mid;
    if(L <= m) update1(L,R,c,lson);
    if(R > m) update1(L,R,c,rson);
    up(rt);
}

ll query(ll L,ll R,ll l,ll r,ll rt){
    if(L > R) return ;
    if(L <= l&&R >= r){
        return mx[rt];
    }
    pushdown(rt);
    mid;
    ll ret = ;
    if(L <= m) ret = max(ret,query(L,R,lson));
    if(R > m) ret = max(ret,query(L,R,rson));
    return ret;
}

struct node{
    ll x,y,a,b;
}v[M];
bool cmp(node aa,node bb){
    if(aa.x == bb.x) return aa.y > bb.y;
    return aa.x < bb.x;
}
ll t[M];
int main()
{
    ll n;
    while(scanf("%lld",&n)!=EOF){
        ll cnt = ;
        for(ll i = ;i <= n;i ++){
            scanf("%lld%lld%lld%lld",&v[i].x,&v[i].y,&v[i].a,&v[i].b);
            t[++cnt] = v[i].y;
        }
        sort(t+,t++cnt);
        sort(v+,v++n,cmp);
        ll m = unique(t+,t++cnt)-t-;
        for(ll i = ;i <= n;i ++)
            v[i].y = lower_bound(t+,t++m,v[i].y)-t+; //离散化时点都向后移一位
        m ++;  //点后移了一位，长度要+1;
        build(,m,);
        for(ll i = ;i <= n;i ++){
            ll ans = query(,v[i].y,,m,);
            update1(v[i].y+,m,v[i].b,,m,);
            update1(,v[i].y-,v[i].a,,m,);
            update(v[i].y,ans+v[i].b,,m,);
        }
        printf("%lld\n",mx[]);
    }
    return ;
}