AcWing：144. 最长异或值路径（dfs + 01字典树）

给定一个树，树上的边都具有权值。

树中一条路径的异或长度被定义为路径上所有边的权值的异或和：

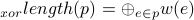
⊕ 为异或符号。

给定上述的具有n个节点的树，你能找到异或长度最大的路径吗？

输入格式

第一行包含整数n，表示树的节点数目。

接下来n-1行，每行包括三个整数u，v，w，表示节点u和节点v之间有一条边权重为w。

输出格式

输出一个整数，表示异或长度最大的路径的最大异或和。

数据范围

1≤n≤1000001≤n≤100000,
0≤u,v<n0≤u,v<n,
0≤w<2310≤w<231

输入样例：

4
0 1 3
1 2 4
1 3 6

输出样例：

7

样例解释

样例中最长异或值路径应为0->1->2,值为7 (=3 ⊕ 4)

算法：dfs + 01字典树

题解：设 D[x] 表示根节点到 x 的路径上所有边权的 xor 值 , 显然有:

D[x] = D[father(x) ] xor weight(x,father(x))

根据上式，我们可以使用dfs，从根节点开始遍历，依次记录每条路径。

又相同的两个数的异或和为0，那么，只要把所求的D[x] 数组像求最大异或对一样就行（最大异或对：https://www.cnblogs.com/buhuiflydepig/p/11306057.html）。

你需要知道它是一棵树。

例如：0 -> 1 -> 2 -> 5 的结果是 4，存再D[5]中。

　　　0 -> 1 的结果是1，存在D[1]中。

现在我们需要求1 -> 5 的结果，就只要把D[1] ^ D[5]就行了，相同的地方异或为0，根据这条性质，就可以得出结果。

#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;

const int maxn = 1e5+;

vector<pair<int, int> > g[maxn];
int tree[maxn * ][];
int d[maxn];
int tot;

void dfs(int u, int fa) {
    int len = g[u].size();
    for(int i = ; i < len; i++) {
        pair<int, int> v = g[u][i];
        if(v.first != fa) {
            d[v.first] = d[u] ^ v.second;
            dfs(v.first, u);
        }
    }
}

void insert(int x) {
    int root = ;
    for(int i = ; i >= ; i--) {
        int idx = (x >> i) & ;
        if(tree[root][idx] == ) {
            tree[root][idx] = ++tot;
        }
        root = tree[root][idx];
    }
}

int search(int x) {
    int root = ;
    int res = ;
    for(int i = ; i >= ; i--) {
        int idx = (x >> i) & ;
        if(tree[root][ ^ idx] != ) {
            root = tree[root][ ^ idx];
            res |= ( << i);
        } else {
            root = tree[root][idx];
        }
    }
    return res;
}

int main() {
    int n;
    scanf("%d", &n);
    for(int i = ; i < n - ; i++) {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        g[u].push_back(make_pair(v, w));
        g[v].push_back(make_pair(u, w));
    }
    dfs(, -);
    int ans = ;
    for(int i = ; i < n; i++) {
        insert(d[i]);
        ans = max(ans, search(d[i]));
    }
    cout << ans << endl;
    return ;
}