noi.ac #529 神树的矩阵

题目链接：戳我

当 \(max(n, m) \ge 3\) 时，可以如下构造：

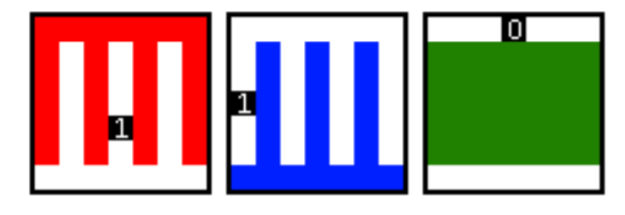
考虑下面这样三个矩阵，红 + 蓝 − 绿得到的矩阵是一个第一行和最后一行全是 1，其他地方全是 0 的矩阵。

那么如果需要把中间某个位置变成 1，可以在红或蓝矩阵中的对应位置加一个 1。

如果需要把第一行或最后一行某个位置变成 0，可以在绿矩阵中的对应位置加一个 1。





然后对于其他情况分别特判就行了（具体哪些可以看main函数）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define MAXN 510
#define mp make_pair
using namespace std;
int n,m;
int move_x[4]={0,0,1,-1},move_y[4]={1,-1,0,0};
char s[MAXN][MAXN];
namespace subtask_0
{
    inline bool check()
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                if(s[i][j]=='1')
                    return false;
        return true;
    }
}
namespace subtask_1
{
    int done[MAXN][MAXN];
    inline bool bfs(int x,int y)//不带done的清空操作
    {
        queue<pair<int,int> >q;
        q.push(mp(x,y));
        while(!q.empty())
        {
            int u_x=q.front().first;
            int u_y=q.front().second;
            q.pop();
            done[u_x][u_y]=1;
            for(int k=0;k<=3;k++)
            {
                int xx=u_x+move_x[k];
                int yy=u_y+move_y[k];
                if(xx<1||xx>n||yy<1||yy>m||s[xx][yy]=='0'||done[xx][yy]) continue;
                done[xx][yy]=1;
                q.push(mp(xx,yy));
            }
        }
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                if(s[i][j]=='1'&&done[i][j]==0) return false;
        return true;
    }
    inline bool check()
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                if(s[i][j]=='1')
                {
                    if(bfs(i,j)==true) return true;
                    else return false;
                }
    }
    inline void solve()
    {
        printf("1\n+\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                printf("%c",s[i][j]);
            puts("");
        }
    }
}
namespace subtask_2
{
    int cnt,cur_ans,pos;
    int fa[MAXN*MAXN],id[MAXN][MAXN];
    map<int,int>ex;
    set<int>sset[MAXN*MAXN];
    inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
    inline bool check()
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                id[i][j]=++cnt,fa[cnt]=cnt;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                for(int k=0;k<=3;k++)
                    {
                        int xx=i+move_x[k];
                        int yy=j+move_y[k];
                        if(xx<1||xx>n||yy<1||yy>m||s[i][j]!=s[xx][yy]) continue;
                        int t=find(id[i][j]),tt=find(id[xx][yy]);
                        if(t!=tt) fa[t]=tt;
                    }
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            {
                if(s[i][j]=='0') continue;
                int t=find(id[i][j]);
                if(!ex.count(t)) ex[t]=1,cur_ans++;
            }
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            {
                if(s[i][j]=='0')
                    for(int k=0;k<=3;k++)
                    {
                        int xx=i+move_x[k];
                        int yy=j+move_y[k];
                        if(xx<1||xx>n||yy<1||yy>m||s[xx][yy]=='0') continue;
                        int t=find(id[i][j]),tt=find(id[xx][yy]);
                        sset[t].insert(tt);
                    }
            }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                if(s[i][j]=='0')
                {
                    int t=find(id[i][j]);
                    if((int)sset[t].size()==cur_ans)
                    {
                        pos=t;
                        break;
                    }
                }
            if(pos!=0) break;
        }
        if(pos==0) return false;
        return true;
    }
    inline void solve()
    {
        printf("2\n+\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(s[i][j]=='1'||(s[i][j]=='0'&&find(id[i][j])==pos)) printf("1");
                else printf("0");
            }
            puts("");
        }
        printf("-\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(s[i][j]=='0'&&find(id[i][j])==pos) printf("1");
                else printf("0");
            }
            puts("");
        }
    }
}
inline void solve_n_1()
{
    vector<pair<int,int> >vec;
    int now=1;
    while(now<=m)
    {
        int cnt1,cnt2;
        while(now<=m&&s[1][now]=='0') now++;
        if(now<=m&&s[1][now]=='1')
        {
            cnt1=now;
            while(now<=m&&s[1][now]=='1') now++;
            cnt2=now-1;
            vec.push_back(mp(cnt1,cnt2));
        }
    }
    printf("%d\n",(int)vec.size());
    for(int i=0;i<vec.size();i++)
    {
        printf("+\n");
        for(int j=1;j<=m;j++)
        {
            if(vec[i].first<=j&&j<=vec[i].second) printf("1");
            else printf("0");
        }
        puts("");
    }
}
inline void solve_m_1()
{
    vector<pair<int,int> >vec;
    int now=1;
    while(now<=n)
    {
        int cnt1,cnt2;
        while(now<=n&&s[now][1]=='0') now++;
        if(now<=n&&s[now][1]=='1')
        {
            cnt1=now;
            while(now<=n&&s[now][1]=='1') now++;
            cnt2=now-1;
            vec.push_back(mp(cnt1,cnt2));
            // printf("[%d %d]\n",cnt1,cnt2);
        }
    }
    printf("%d\n",(int)vec.size());
    for(int i=0;i<vec.size();i++)
    {
        printf("+\n");
        for(int j=1;j<=n;j++)
        {
            if(vec[i].first<=j&&j<=vec[i].second) printf("1\n");
            else printf("0\n");
        }
        // puts("");
    }
}
namespace others
{
    char t[MAXN][MAXN],r[MAXN][MAXN],q[MAXN][MAXN];
    inline void print()
    {
        printf("3\n");
        printf("+\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                printf("%c",t[i][j]);
            puts("");
        }
        printf("+\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                printf("%c",r[i][j]);
            puts("");
        }
        printf("-\n");
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                printf("%c",q[i][j]);
            puts("");
        }
    }
    inline void solve_m_2()
    {
        for(int i=1;i<=n;i++)
        {
            t[i][1]='1';
            t[i][2]=(s[i][2]=='1'?'1':'0');
        }
        for(int i=1;i<=n;i++)
        {
            r[i][2]='1';
            r[i][1]=(s[i][1]=='1'?'1':'0');
        }
        for(int i=1;i<=n;i++) q[i][1]=q[i][2]='1';
        print();
    }
    inline void solve()
    {
        for(int i=1;i<=n;i++)
        {
            t[i][1]='1',t[i][m]='0';
            r[i][1]='0',r[i][m]='1';
            for(int j=2;j<m;j++) t[i][j]=r[i][j]=s[i][j];
            if(i&1)
                for(int j=1;j<m;j++) t[i][j]='1';
            else
                for(int j=2;j<=m;j++) r[i][j]='1';
        }
        for(int i=1;i<=n;i++)
        {
            q[i][1]=(s[i][1]=='0'?'1':'0');
            q[i][m]=(s[i][m]=='0'?'1':'0');
            for(int j=2;j<m;j++) q[i][j]='1';
        }
        print();
    }
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("ce.in","r",stdin);
    // freopen("ce.out","w",stdout);
    #endif
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
    if(subtask_0::check()) printf("0\n");
    else if(subtask_1::check()) subtask_1::solve();
    else if(subtask_2::check()) subtask_2::solve();
    else if(n==1) solve_n_1();
    else if(m==1) solve_m_1();
    else if(m==2) others::solve_m_2();
    else others::solve();
    return 0;
}