[译]2D空间中使用四叉树Quadtree进行碰撞检测优化

操作系统:Windows8.1

显卡:Nivida GTX965M

开发工具：Unity2017.2.0f3

---

原文出处 ： Quick Tip: Use Quadtrees to Detect Likely Collisions in 2D Space

许多游戏需要使用碰撞检测算法去判定两个对象是否发生碰撞，但是这些算法通常意味着昂贵操作，拖慢游戏的运行速度。在这篇文章中我们将会学习四叉树 quadtrees，并学习如果通过四叉树跳过那些物理空间距离比较远的对象，最终提高碰撞检测速度。

注：原文中使用Java实现，但是考虑目前多产品是基于Unity3D，故采用C#进行相关实现说明。

IntroDuction

---

碰撞检测 Collision detection 对于视频游戏来说是非常必要的。无论是2D游戏或是3D游戏中，正确的检测两个物体发生碰撞检测非常重要，否则会出现一切有趣的效果：

然而，碰撞检测是一种非常昂贵的操作。假设有100个对象需要进行碰撞检测时。每两个对象进行比较：100 x 100 = 10000 次，检测的次数实在太多，消耗大量CPU资源。

一种优化途径是减少非必要的碰撞检测的数量。比如屏幕两端的两个物体位于上下两侧，是不可能发生碰撞检测，因此不需要检测它们之间的碰撞。这正是四叉树发挥作用的地方。

What Is a Quadtree?

---

一个四叉树 quadtree 是一种将2D区域划分为更易于管理的数据结构。他是基于二叉树 binary tree 的扩展，采用四个节点代替两个节点。

在下面的图示中，每个图像是2D空间的一个可视化呈现，红色方块表示对象物体。同时为了更好的说明问题，子节点按照逆时针顺序标记。

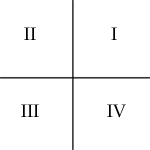
一个四叉树开始于单节点(根节点)。此时的根节点还没有进行2D空间的分隔，故添加到四叉树的对象被添加到单节点里。

当更多的对象添加到四叉树时，他最终会进行分裂为四个子节点的形态。每个对象会会根据他们在2D空间中的位置划分到这些子节点中。任何不能完全适合子节点内部边界规则的对象将会被放置在父节点中。

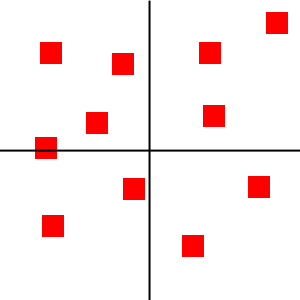
随着对象数量的增加，每个子节点可以继续分裂。

如图所示，每个节点只能包含有限的对象。同时我们了解到，左上角节点中的对象不能与右下角节点中的对象发生碰撞，所以我们不需要在这些节点之间进行昂贵的碰撞检测算法。

Take a look at this JavaScript example 基于Javascript实现的四叉树案例。

Implementing a Quadtree

---

实现四叉树相对比较简单、容易。下面的代码采用C#编写，注原文基于Java。但是无论啥语言实现理念都是一致的，另外会在每个代码块之后进行注释说明。

我们从创建四叉树的核心类 Quadtree 开始。代码如下所示：

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

public class QuadTree {

    private int MAX_OBJECTS = ;
    private int MAX_LEVELS = ;

    private int level;
    private List<SquareOne> objects;
    private Rect bounds;
    private QuadTree[] nodes;

    public QuadTree (int pLevel, Rect pBounds)
    {
        level = pLevel;
        objects = new List<SquareOne>();
        bounds = pBounds;
        nodes = new QuadTree[];
    }
｝

这个类的看上去是比较直观的， MAX_OBJECTS 定义了一个节点所能持有的最大对象数量，如果超过则进行分裂。 MAX_LEVELS 定义了子节点的最大深度。level 是当前节点深度 ( 0 代表最上层节点 )， bounds 代表2D空间的区域面积， 最后 nodes 代表四个子节点的集合。

在这个例子中，四叉树可以容纳的对象是基于矩形形状 Rectangles 的，但是没有任何限制进行自定义。

下面我们实现四叉树的核心五个函数，分别为： Clear ， Split ， GetIndex ， Insert 和 Retrieve 。

// Clear quadtree
    public void Clear()
    {
        objects.Clear();

        for(int i  = ; i < nodes.Length; i++)
        {
            if(nodes[i] != null)
            {
                nodes[i].Clear();
                nodes[i] = null;
            }
        }
    }

该 Clear 函数基于递归的思路清理四叉树每个节点及节点中的对象集合。

// Split the node into 4 subnodes
    private void Split()
    {
        int subWidth = (int)(bounds.width / );
        int subHeight = (int)(bounds.height / );
        int x = (int)bounds.x;
        int y = (int)bounds.y;

        nodes[] = new QuadTree(level + , new Rect(x + subWidth, y, subWidth, subHeight));
        nodes[] = new QuadTree(level + , new Rect(x, y, subWidth, subHeight));
        nodes[] = new QuadTree(level + , new Rect(x, y + subHeight, subWidth, subHeight));
        nodes[] = new QuadTree(level + , new Rect(x + subWidth, y + subHeight, subWidth, subHeight));
    }

该 Split 函数用于将当前节点分裂为四个子节点，并对四个节点进行边界裁剪的初始化操作。

private List<int> GetIndexes(Rect pRect)
    {

        List<int> indexes = new List<int>();

        double verticalMidpoint = bounds.x + (bounds.width / );
        double horizontalMidpoint = bounds.y + (bounds.height / );

        bool topQuadrant = pRect.y >= horizontalMidpoint;
        bool bottomQuadrant = (pRect.y - pRect.height) <= horizontalMidpoint;
        bool topAndBottomQuadrant = pRect.y + pRect.height +  >= horizontalMidpoint && pRect.y +  <= horizontalMidpoint;

        if(topAndBottomQuadrant)
        {
            topQuadrant = false;
            bottomQuadrant = false;
        }

        // Check if object is in left and right quad
        if(pRect.x + pRect.width +  >= verticalMidpoint && pRect.x - <= verticalMidpoint)
        {
            if(topQuadrant)
            {
                indexes.Add();
                indexes.Add();
            }
            else if(bottomQuadrant)
            {
                indexes.Add();
                indexes.Add();
            }
            else if(topAndBottomQuadrant)
            {
                indexes.Add();
                indexes.Add();
                indexes.Add();
                indexes.Add();
            }
        }

        // Check if object is in just right quad
        else if(pRect.x +  >= verticalMidpoint)
        {
            if(topQuadrant)
            {
                indexes.Add();
            }
            else if(bottomQuadrant)
            {
                indexes.Add();
            }
            else if(topAndBottomQuadrant)
            {
                indexes.Add();
                indexes.Add();
            }
        }
        // Check if object is in just left quad
        else if(pRect.x - pRect.width <= verticalMidpoint)
        {
            if(topQuadrant)
            {
                indexes.Add();
            }
            else if(bottomQuadrant)
            {
                indexes.Add();
            }
            else if(topAndBottomQuadrant)
            {
                indexes.Add();
                indexes.Add();
            }
        }
        else
        {
            indexes.Add(-);
        }

        return indexes;
    }

该 GetIndex 是四叉树内部的辅助函数。他决定了四叉树中一个对象属于哪个节点，最终将该对象划分到该节点中。

public void Insert(SquareOne sprite)
    {
        SquareOne fSprite = sprite;
        Rect pRect = fSprite.GetTextureRectRelativeToContainer();

        if(nodes[] != null)
        {
            List<int> indexes = GetIndexes(pRect);
            for(int ii = ; ii < indexes.Count; ii++)
            {
                int index = indexes[ii];
                if(index != -)
                {
                    nodes[index].Insert(fSprite);
                    return;
                }
            }

        }

        objects.Add(fSprite);

        if(objects.Count > MAX_OBJECTS && level < MAX_LEVELS)
        {
            if(nodes[] == null)
            {
                Split();
            }

            int i = ;
            while(i < objects.Count)
            {
                SquareOne sqaureOne = objects[i];
                Rect oRect = sqaureOne.GetTextureRectRelativeToContainer();
                List<int> indexes = GetIndexes(oRect);
                for(int ii = ; ii < indexes.Count; ii++)
                {
                    int index = indexes[ii];
                    if (index != -)
                    {
                        nodes[index].Insert(sqaureOne);
                        objects.Remove(sqaureOne);
                    }
                    else
                    {
                        i++;
                    }
                }
            }
        }
    }

该 Insert 是每个加入四叉树的对象要执行的函数。该方法首先确定节点是否有子节点，并尝试向子节点添加对象。如果没有子节点或者对象根据边界规则不适合任何子节点的插入操作，则将对象划分到父节点中。

一旦对象添加到某一个节点中，该节点需要进一步判断当前持有的对象数量 是否 超过最大对象持有对象数量，如果是则进行分化。分化节点会导致该节点插入的所有对象重新划分到子节点的操作，如果不满足边界规则，则将对象保留在父节点中。

private List<SquareOne> Retrieve(List<SquareOne> fSpriteList, Rect pRect)
    {
        List<int> indexes = GetIndexes(pRect);
        for(int ii = ; ii < indexes.Count; ii++)
        {
            int index = indexes[ii];
            if(index != - && nodes[] != null)
            {
                nodes[index].Retrieve(fSpriteList, pRect);
            }    

            fSpriteList.AddRange(objects);
        }

        return fSpriteList;
    }

最后一个 Retrieve 函数，他根据输入的对象返回所有可能发生碰撞的对象集合。该方法将有助于极爱年少碰撞检测对的数量。

Using This for 2D Collision Detection

---

现在我们已经实现了完整的四叉树，是时候使用他帮助我们减少碰撞检测的数量。

在典型的游戏场景中，我们需要根据传递的 Screen 屏幕边界尺寸来创建合适的四叉树对象。

Quadtree quad = new Quadtree(, new Rect(,,,));

在游戏每一帧中，清理四叉树，然后使用 Insert 函数将所有的对象到添加到四叉树中。

当所有的对象添加完毕，你会遍历每个对象，并检索它可能碰撞的对象列表。然后使用碰撞检测算法检查列表中的每个对象与初始对象之间是否真的发生碰撞。

List returnObjects = new List<SqureOne>();
for (int i = ; i < allObjects.size(); i++) {
  returnObjects.Clear();
  quad.Retrieve(returnObjects, objects.get(i));

  for (int x = ; x < returnObjects.size(); x++) {
    // Run collision detection algorithm between objects
  }
}

注意：碰撞检测的算法已经超出了本文的讨论范围，这里有一个 文章 进行学习。

Conclusion

---

碰撞检测通常是一种比较昂贵的操作，可能会对游戏的性能造成挑战。四叉树是一种加速碰撞检测过程的途径，最终使得游戏运行更加流畅。