基于梯度场和Hessian特征值分别获得图像的方向场
一、我们想要求的方向场的定义为:
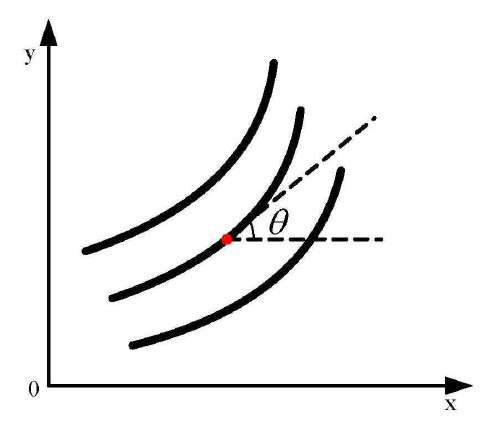
 ,表示x方向的梯度和y方向的梯度
,表示x方向的梯度和y方向的梯度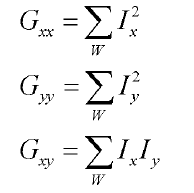
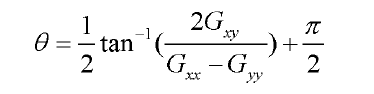
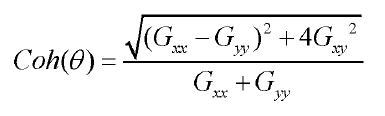
normalize(matCoh,matCoh,0,1,NORM_MINMAX);



frangi2d(img,J,Scale,directions,opts);

基于梯度场和Hessian特征值分别获得图像的方向场的更多相关文章
- MATLAB绘制等高线和梯度场
clear;clc;close all [X,Y] = meshgrid(-:.:); % 产生网格数据X和Y Z = X.*exp(-X.^ - Y.^); % 计算网格点处曲面上的Z值 [DX,D ...
- 4.基于梯度的攻击——MIM
MIM攻击原论文地址——https://arxiv.org/pdf/1710.06081.pdf 1.MIM攻击的原理 MIM攻击全称是 Momentum Iterative Method,其实这也是 ...
- 2.基于梯度的攻击——FGSM
FGSM原论文地址:https://arxiv.org/abs/1412.6572 1.FGSM的原理 FGSM的全称是Fast Gradient Sign Method(快速梯度下降法),在白盒环境 ...
- 3 基于梯度的攻击——MIM
MIM攻击原论文地址——https://arxiv.org/pdf/1710.06081.pdf 1.MIM攻击的原理 MIM攻击全称是 Momentum Iterative Method,其实这也是 ...
- 1 基于梯度的攻击——FGSM
FGSM原论文地址:https://arxiv.org/abs/1412.6572 1.FGSM的原理 FGSM的全称是Fast Gradient Sign Method(快速梯度下降法),在白盒环境 ...
- 数字图像处理-基于matlab-直方图均匀化,傅立叶变换,图像平滑,图像锐化
直方图均匀化 任务:用MATLAB或VC或Delphi等实现图像直方图均匀化的算法. clc;clear;close all; % 清除工作台 % path(path,'..\pics'); % 设置 ...
- C / C ++ 基于梯度下降法的线性回归法(适用于机器学习)
写在前面的话: 在第一学期做项目的时候用到过相应的知识,觉得挺有趣的,就记录整理了下来,基于C/C++语言 原贴地址:https://helloacm.com/cc-linear-regression ...
- 3.基于梯度的攻击——PGD
PGD攻击原论文地址——https://arxiv.org/pdf/1706.06083.pdf 1.PGD攻击的原理 PGD(Project Gradient Descent)攻击是一种迭代攻击,可 ...
- 2 基于梯度的攻击——PGD
PGD攻击原论文地址——https://arxiv.org/pdf/1706.06083.pdf 1.PGD攻击的原理 PGD(Project Gradient Descent)攻击是一种迭代攻击,可 ...
随机推荐
- 为什么使用eval()将json字符串转换为对象要多加一个小括号
使用eval()将json字符串转换为对象要多加一个小括号: 关于eval()函数的具体用法这里就不多介绍了,具体可以参阅javascript的eval()方法一章节,下面就介绍一下为什么使用eval ...
- c++11实现异步定时器
c++11提供了丰富的时间和线程操作函数,比如 std::this_thread::sleep, std::chrono::seconds等.可以利用这些来很方便的实现一个定时器. 定时器要求 ...
- Linux就是这个范儿之第一次亲密接触(2)
原创作品,允许转载,转载时请务必以超链接形式标明文章原始出处 .作者信息和本声明.否则将追究法律责 1.2 不一样的图形操作 几乎所有Linux的新用户都会认为Linux的图形界面是相当的绚丽又多彩. ...
- java基础---->多线程之interrupt(九)
这里我们通过实例来学习一下java多线程中关于interrupt方法的一些知识.执者失之.我想当一个诗人的时候,我就失去了诗,我想当一个人的时候,我就失去了我自己.在你什么也不想要的时候,一切如期而来 ...
- js插件---->jquery通知插件toastr的使用
toastr是一款非常棒的基于jquery库的非阻塞通知提示插件,toastr可设定四种通知模式:成功,出错,警告,提示,而提示窗口的位置,动画效果都可以通过能数来设置.toastr需要jquery的 ...
- luogu P2066 机器分配[背包dp+方案输出]
题目背景 无 题目描述 总公司拥有高效设备M台,准备分给下属的N个分公司.各分公司若获得这些设备,可以为国家提供一定的盈利.问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值.其中M≤15 ...
- 服务器报错 500,请确保 ASP.NET State Service(ASP.NET 状态服务)已启动
报错信息: 解决方案: 开启此服务
- Linux系统下tomcat安装配置
Linux系统中Tomcat的安装配置. 前提JDK已经安装好. 安装 下载tomcatwget http://mirrors.cnnic.cn/apache/tomcat/tomcat-8/v8.0 ...
- 【git】------git的基本介绍及linux的基本命令------【巷子】
001.git简介 git是一款开源的分布式版本控制工具 在世界上所有的分布式版本控制工具中,git是最快.最简单.最流行的 git的起源 作者是Linux之父:Linus Benedict Torv ...
- python2在安装pywin32后出现ImportError: DLL load failed 解决方法
python2在安装pywin32后出现ImportError: DLL load failed 解决方法 在python2中有时候会出现: import win32api ImportError ...
