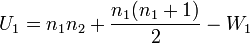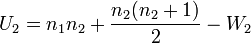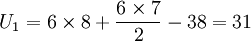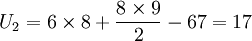曼慧尼特u检验(两个样本数据间有无差异)
曼-惠特尼U检验(Mann-Whitney检验)
How the Mann-Whitney test works
Mann-Whitney检验又叫做秩和检验,是比较没有配对的两个独立样本的非参数检验。思想是这样的:假定要检验两组数据之间有没有差异。首先,不管分组把所有数据排序。按照数值大小给定一个值叫做秩。最小的值秩为1,最大的为N(假定两个样本总共有N个观察值)。如果有相同的值,就得到相同的秩。相同的值的秩是他们的秩的平均值。如果两组的秩的和差距比较大,就会得出较小的p值,认为这两组间有显著差异。
How to think about the results of a Mann-Whitney test
样本量太小的话效度会很低。比如,如果总的数据只有7个或者更少的话,p值总是大于5%的。
Is the Mann-Whitney test the right test for these data?
分析之前要先看一下,Mann-Whitney 检验是否适合手头的问题。
|
问题 |
解释 |
|
“误差”是独立的吗? |
“误差”指的是每个值和中位数的差异。仅当误差的分布是随机的时候Mann-Whitney 检验的结果才有意义。一般要保证独立样本。样本不独立可能会导致误差不随机。 |
|
数据是配对的吗? |
如果数据是配对的,应该用Wilcoxon成对检验。 |
|
是只比较两组数据吗? |
Mann-Whitney 检验只用于两组数据的比较。如果要比较多组数据,可以用 Kruskal-Wallis 检验。用几次 Mann-Whitney 检验来比较多个组间的差异是不适合的,就如同ANOVA 不能用多次t检验代替一样。 |
|
两个分布的形状是相同的吗? |
Mann-Whitney 检验不需要假定数据符合某种分布,但是要求两个分布是相同的。如果两组的分布差异比较大,可能需要数据转换使之相近。 |
|
是否比较中位数? |
Mann-Whitney 检验比较的是两组的中位数。 |
|
数据分布时正态的吗? |
非参数检验的好处和弱点是不需要假定数据符合某种分布。非参数检验有时候更适合(当数据分布未知时),有时候效度较低(当已知分布时参数检验效度更高)。所以如果数据能够转换为正态分布,t检验将会有更高的效度。 |
曼-惠特尼U检验的步骤
Computation of the U test begins by arbitrarily designating two samples as group 1 and group 2.the data from the two groups are combined into one group ,with each data value retaining a group identifier of its original group.the pooled values are then ranked from 1 to n,with the smallest value being assigned a rank of 1.
The sum of the ranks of Values from group 1 is computed and designated as W1 and the sum of the ranks of values from group 2 is designated as W2.[1]
该方法的具体步骤如下:
第一步:将两组数据混合,并按照大小顺序编排等级。最小的数据等级为1,第二小的数据等级为2,以此类推(若有数据相等的情形,则取这几个数据排序的平均值作为其等级)。
第二步:分别求出两个样本的等级和W1、W2。
第三步:计算曼-惠特尼U检验统计量,n1为第一个样本的量,n2为第二个样本的量:
选择U1和U2中最小者与临界值Uα比较,当U < UA时,拒绝H0,接受H1。
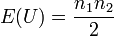
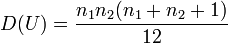
当n1和n2都不小于10时,随机变量近似服从正态分布。
第四步:作出判断。
设第一个总体的均值为μ1,第二个总体的均值为μ2,则有:
1)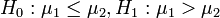 ,如果Z < − Zα,则拒绝H0;
,如果Z < − Zα,则拒绝H0;
2)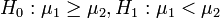 ,如果Z > Zα,则拒绝H0;
,如果Z > Zα,则拒绝H0;
3)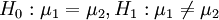 ,如果Z > − Zalpha / 2,则拒绝H0。
,如果Z > − Zalpha / 2,则拒绝H0。
曼-惠特尼U检验的应用举例
下面是两种不同加工方式的菜粕在黄牛瘤胃内培养16h的干物质降解率,用曼-惠特尼U检验比较其有无差异:
两种加工方式的菜粕瘤胃培养16h的干物质降解率(%)
| 预压浸出组 | 等级排序 | 螺旋热榨组 | 等级排序 |
|---|---|---|---|
| 39.33 | 3 | 42.91 | 5 |
| 44.10 | 8 | 44.69 | 10 |
| 35.89 | 1 | 44.54 | 9 |
| 43.35 | 6 | 45.31 | 11 |
| 47.61 | 13 | 37.73 | 2 |
| 43.71 | 7 | 48.75 | 14 |
| 46.71 | 12 | ||
| 41.85 | 4 |
先按照大小顺序排列等级(见上表),而后计算W1 = 38,W2 = 67,n1 = 6,n2 = 8。
假设两种菜粕的16h瘤胃干物质降解率除了平均水平以外在其它方面无差异,即检验:
- H0:两种菜粕的16h瘤胃干物质降解率无差异;
- H1:两种菜粕的16h瘤胃干物质降解率有差异。
计算U值:
U2值较小,选取U2与Uα(α=0.05)比较,通过查表(附表)可知Uα = 8,U2 > Uα,即接受H0,认为两种加工方式的菜粕瘤胃培养16h的干物质降解率无显著差异。
| n2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 | |||||||||||||||
| 1 | |||||||||||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||||||
| 3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | ||||
| 4 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 5 | 0 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | ||
| 6 | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | ||
| 7 | 1 | 3 | 5 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | ||
| 8 | 0 | 2 | 4 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 22 | 24 | 26 | 29 | |
| 9 | 0 | 2 | 4 | 7 | 10 | 12 | 15 | 17 | 20 | 23 | 26 | 28 | 31 | 34 | |
| 10 | 0 | 3 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | 33 | 36 | 39 | |
| 11 | 0 | 3 | 6 | 9 | 13 | 16 | 19 | 23 | 26 | 30 | 33 | 37 | 40 | 44 | |
| 12 | 1 | 4 | 7 | 11 | 14 | 18 | 22 | 26 | 29 | 33 | 37 | 41 | 45 | 49 | |
| 13 | 1 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 33 | 37 | 41 | 45 | 50 | 54 | |
| 14 | 1 | 5 | 9 | 13 | 17 | 22 | 26 | 31 | 36 | 40 | 45 | 50 | 55 | 59 | |
| 15 | 1 | 5 | 10 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 |
| n2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 | |||||||||||||||
| 1 | |||||||||||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||||||
| 3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | ||||
| 4 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 5 | 0 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | ||
| 6 | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | ||
| 7 | 1 | 3 | 5 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | ||
| 8 | 0 | 2 | 4 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 22 | 24 | 26 | 29 | |
| 9 | 0 | 2 | 4 | 7 | 10 | 12 | 15 | 17 | 20 | 23 | 26 | 28 | 31 | 34 | |
| 10 | 0 | 3 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | 33 | 36 | 39 | |
| 11 | 0 | 3 | 6 | 9 | 13 | 16 | 19 | 23 | 26 | 30 | 33 | 37 | 40 | 44 | |
| 12 | 1 | 4 | 7 | 11 | 14 | 18 | 22 | 26 | 29 | 33 | 37 | 41 | 45 | 49 | |
| 13 | 1 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 33 | 37 | 41 | 45 | 50 | 54 | |
| 14 | 1 | 5 | 9 | 13 | 17 | 22 | 26 | 31 | 36 | 40 | 45 | 50 | 55 | 59 | |
| 15 | 1 | 5 | 10 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 |
| n2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 | |||||||||||||||
| 1 | |||||||||||||||
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||||||
| 3 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | ||||
| 4 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 5 | 0 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | ||
| 6 | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | ||
| 7 | 1 | 3 | 5 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | ||
| 8 | 0 | 2 | 4 | 6 | 8 | 10 | 13 | 15 | 17 | 19 | 22 | 24 | 26 | 29 | |
| 9 | 0 | 2 | 4 | 7 | 10 | 12 | 15 | 17 | 20 | 23 | 26 | 28 | 31 | 34 | |
| 10 | 0 | 3 | 5 | 8 | 11 | 14 | 17 | 20 | 23 | 26 | 29 | 33 | 36 | 39 | |
| 11 | 0 | 3 | 6 | 9 | 13 | 16 | 19 | 23 | 26 | 30 | 33 | 37 | 40 | 44 | |
| 12 | 1 | 4 | 7 | 11 | 14 | 18 | 22 | 26 | 29 | 33 | 37 | 41 | 45 | 49 | |
| 13 | 1 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 33 | 37 | 41 | 45 | 50 | 54 | |
| 14 | 1 | 5 | 9 | 13 | 17 | 22 | 26 | 31 | 36 | 40 | 45 | 50 | 55 | 59 | |
| 15 | 1 | 5 | 10 | 14 | 19 | 24 | 29 | 34 | 39 | 44 | 49 | 54 | 59 | 64 |
曼慧尼特u检验(两个样本数据间有无差异)的更多相关文章
- 检验两个随机序列的beta系数
检验两个随机序列的beta系数 代码 def test_beta(loops=10): ''' 检验两个随机序列的beta系数 :loops: int, 循环次数, 每次循环会产生两个随机序列, 然后 ...
- Unix系统中,两个进程间的通信
进程之间通常需要进行数据的传输或者共享资源等,因此进程间需要通讯. 可以通过管道,信号,消息队列,共享内存,信号量和套接字等方式 FIFO表示命名管道,这种管道的操作是基于先进先出原理. PIPE 表 ...
- C# 调用Windows API实现两个进程间的通信
使用Windows API实现两个进程间(含窗体)的通信http://blog.csdn.net/huangxinfeng/article/details/5513608 从C#下使用WM_COPYD ...
- 【Linux学习笔记】用nc实现两台主机间的文件传输(不需要输密码)
通常,可以用scp完成两台主机间的文件传输任务,但在主机间未建立信任关系的情况下,scp每次都需要输入密码,用起来感觉不是很方便,之前这篇笔记介绍过不用输入密码执行脚本或传输文件的方法,但对于一些临时 ...
- openStack 重新resize时会进行重新调度,可能在本机Resize 扩展资源,也可能存在的情况时 ,新扩展的资源在当前节点不足分配,整个虚拟机将进行迁移调度,进行异机迁移时需要迁移 的两台主机间能使用nova系统用户经passless登录
openStack 重新resize时会进行重新调度,可能在本机Resize 扩展资源,也可能存在的情况时 ,新扩展的资源在当前节点不足分配,整个虚拟机将进行迁移调度,进行异机迁移时需要迁移 的两台主 ...
- poj 1789 每个字符串不同的字母数代表两个结点间的权值 (MST)
题目大意是就是给出n个长度为7的字符串,每个字符串代表一个车,定义车的距离是两个字符串间不同字母的个数,题目要求的数不同的车的距离的最小值,即所求的就是最小生成树 Sample Input 4aaaa ...
- git 对比两个commit 之间的差异
git 对比两个commit 之间的差异 比较两个版本之间的差异 git diff commit-id-1 commit-id-2 > d:/diff.txt 结果文件diff.txt中: &q ...
- 让两个对象间建立weak关系
让两个对象间建立weak关系 这是为了给两个对象间建立weak关系,当一个对象被释放时,另外一个对象再获取这个值时就是nil,也就是不持有这个对象:) 源码: WeakRelatedDictionar ...
- java实现两台电脑间TCP协议文件传输
记录下之前所做的客户端向服务端发送文件的小项目,总结下学习到的一些方法与思路. 注:本文参考自<黑马程序员>视频. 首先明确需求,在同一局域网下的机器人A想给喜欢了很久的机器人B发送情书, ...
随机推荐
- [原]openstack-kilo--issue(七):虚拟机怎么通外网,外网怎么ping通虚拟机
=====问题======= 虚拟机可以ping通外网,外网能ping通虚拟机但是收不到reply 这个问题本人遇到有两种情况: 1.安装完整openstack-kilo后,在route中和虚拟机中抓 ...
- android 反编译apktool工具
下载地址:http://pan.baidu.com/s/1bnHANtd 1.将编译的*.apk放在apktool的根目录下:2.双击“解压软件.bat”后,会提示完成:这样就反编译成功以:3.查看反 ...
- myeclipse优化
myeclipse优化 http://blog.163.com/cayyenne@126/blog/static/12186261420100611546658/
- web进阶之jQuery操作DOM元素&&MySQL记录操作&&PHP面向对象学习笔记
hi 保持学习数量和质量 1.jQuery操作DOM元素 ----使用attr()方法控制元素的属性 attr()方法的作用是设置或者返回元素的属性,其中attr(属性名)格式是获取元素属性名的值,a ...
- 150925-周五不干活-HTML(CSS),Javascript
不干活就干自己.. 今天所有代码总结为一个如下 <!DOCTYPE HTML><html><head><meta http-equiv="Conte ...
- POJ1386Play on Words[有向图欧拉路]
Play on Words Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 11846 Accepted: 4050 De ...
- AC日记——计算多项式的导函数 openjudge 1.5 38
38:计算多项式的导函数 总时间限制: 1000ms 内存限制: 65536kB 描述 计算多项式的导函数是一件非常容易的任务.给定一个函数f(x),我们用f'(x)来表示其导函数.我们用x^n来 ...
- 重写成员“log4net.Util.ReadOnlyPropertiesDictionary.GetObjectData(System.Runtime.Serialization.SerializationInfo, System.Runtime.Serialization.StreamingContext)”时违反了继承安全性规则
在.NET 4.0下使用最新版本的log4Net 1.2.10,会遇到下面这样的错误: 重写成员“log4net.Util.ReadOnlyPropertiesDictionary.GetObject ...
- MyBatis配置文件解析
MyBatis配置文件解析(概要) 1.configuration:根元素 1.1 properties:定义配置外在化 1.2 settings:一些全局性的配置 1.3 typeAliases:为 ...
- Android驱动入门-LED--HAL硬件访问服务层②
硬件平台: FriendlyARM Tiny4412 Cortex-A9 操作系统: UBUNTU 14.04 LTS 时间:2016-09-21 16:58:56 为了避免访问冲突,则创建了硬件访 ...