第二章平稳时间序列模型——AR(p),MA(q),ARMA(p,q)模型及其平稳性






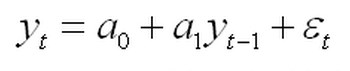


 等于
等于
 等于
等于


 或
或 )
)模型表达式为:(2.16)(截距项不影响平稳性,略去)
设其挑战解为:(用待定系数法)
 (2.17)
(2.17)


 (t很大时用级数求和)
(t很大时用级数求和) 等于
等于

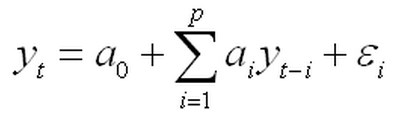




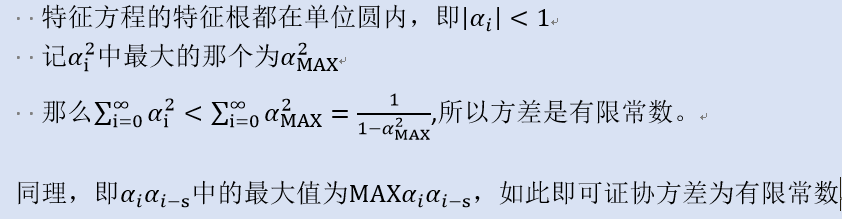
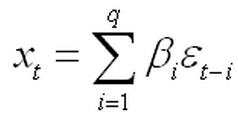


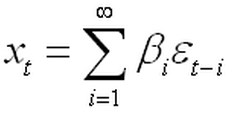

 (2.22)
(2.22) (2.23)
(2.23) 的特征根在单位圆外,则(2.23)的每一项都平稳,所以其和也平稳,所以ARMA(p,q)模型平稳。(书上没再给出更多解释了)
的特征根在单位圆外,则(2.23)的每一项都平稳,所以其和也平稳,所以ARMA(p,q)模型平稳。(书上没再给出更多解释了)第二章平稳时间序列模型——AR(p),MA(q),ARMA(p,q)模型及其平稳性的更多相关文章
- 第二章平稳时间序列模型——ACF和PACF和样本ACF/PACF
自相关函数/自相关曲线ACF AR(1)模型的ACF: 模型为: 当其满足平稳的必要条件|a1|<1时(所以说,自相关系数是在平稳条件下求得的): y(t)和y(t-s)的 ...
- 时间序列算法(平稳时间序列模型,AR(p),MA(q),ARMA(p,q)模型和非平稳时间序列模型,ARIMA(p,d,q)模型)的模型以及需要的概念基础学习笔记梳理
在做很多与时间序列有关的预测时,比如股票预测,餐厅菜品销量预测时常常会用到时间序列算法,之前在学习这方面的知识时发现这方面的知识讲解不多,所以自己对时间序列算法中的常用概念和模型进行梳理总结(但是为了 ...
- ARIMA模型——本质上是error和t-?时刻数据差分的线性模型!!!如果数据序列是非平稳的,并存在一定的增长或下降趋势,则需要对数据进行差分处理!ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数
https://www.cnblogs.com/bradleon/p/6827109.html 文章里写得非常好,需详细看.尤其是arima的举例! 可以看到:ARIMA本质上是error和t-?时刻 ...
- ASP.NET MVC with Entity Framework and CSS一书翻译系列文章之第二章:利用模型类创建视图、控制器和数据库
在这一章中,我们将直接进入项目,并且为产品和分类添加一些基本的模型类.我们将在Entity Framework的代码优先模式下,利用这些模型类创建一个数据库.我们还将学习如何在代码中创建数据库上下文类 ...
- 《Entity Framework 6 Recipes》翻译系列 (3) -----第二章 实体数据建模基础之创建一个简单的模型
第二章 实体数据建模基础 很有可能,你才开始探索实体框架,你可能会问“我们怎么开始?”,如果你真是这样的话,那么本章就是一个很好的开始.如果不是,你已经建模,并在实体分裂和继承方面感觉良好,那么你可以 ...
- 【黑金原创教程】【TimeQuest】【第二章】TimeQuest模型角色,网表概念,时序报告
声明:本文为黑金动力社区(http://www.heijin.org)原创教程,如需转载请注明出处,谢谢! 黑金动力社区2013年原创教程连载计划: http://www.cnblogs.com/al ...
- 时序分析:ARIMA模型(非平稳时间序列)
转载于一篇硕士论文.... ARIMA模型意为求和自回归滑动平均模型(IntergratedAut少regressive MovingAverageModel),简记为ARIMA(p,d,q),p,q ...
- [书籍翻译] 《JavaScript并发编程》 第二章 JavaScript运行模型
本文是我翻译<JavaScript Concurrency>书籍的第二章 JavaScript运行模型,该书主要以Promises.Generator.Web workers等技术来讲解J ...
- KnockoutJS 3.X API 第二章 数据监控(1)视图模型与监控
数据监控 KO的三个内置核心功能: 监控(Observable)和依赖性跟踪(dependency tracking) 声明绑定(Declarative bindings) 模板(Templating ...
随机推荐
- subprocess实现管道
# shell last | cut -d ' ' -f 1 | sort -u #python from subprocess import Popen,PIPE p1 = Popen('last' ...
- C# 获取当前,相对,绝对路径
一.C#获取当前路径的方法: 1. System.Diagnostics.Process.GetCurrentProcess().MainModule.FileName -获取模块的完整路径. 2. ...
- powershell小工具
保存为.ps1文件Set-ExecutionPolicy UnrestrictedSet-ExecutionPolicy Restricted 1. 批量修改文件后缀 $CodeFileDir=&qu ...
- CentOS禁用触摸板
安装xorg-x11-apps包 yum install xorg-x11-apps 查看设备信息 cd /dev/input/ ls //找到触摸板信息 xinput list //找到触摸板的id ...
- UVa 11149 Power of Matrix(倍增法、矩阵快速幂)
题目链接: 传送门 Power of Matrix Time Limit: 3000MS Description 给一个n阶方阵,求A1+A2+A3+......Ak. 思路 A1+A2+. ...
- JavaScript 的错误(Error)与异常(Exception)处理
PHP很少用到错误处理,因为框架帮了大忙,所以基本上没有主动接手过PHP的错误.PHP是偏后端的动态处理语言,和用户的关系不大,所以用户不会关心是否出现了报错.但是JavaScript就非常不同了,j ...
- Vijos1921严厉的班长
传送门 在贴吧上看到了这道题,恰好最近在学相关的东西,觉得比较有意思就去做了. 第一眼看上去比较像搜索,其实是道状压DP.我简单讲一下思路: 首先明确,不管之前取了什么数,取1必定满足所有的数之间互质 ...
- virtualenv中ImportError: No module named django
问题现象:在代码py文件中,import django 报错,但是在python shell中直接执行这个语句没错, 网上搜索了下,自己测试了下,确定原因是由于使用了python中的virtualen ...
- 深入理解javascript中执行环境(作用域)与作用域链
深入理解javascript中执行环境(作用域)与作用域链 相信很多初学者对与javascript中的执行环境与作用域链不能很好的理解,这里,我会按照自己的理解同大家一起分享. 一般情况下,我们把执行 ...
- linux第一面
随着Linux应用的扩展许多朋友开始接触Linux,根据学习Windwos的经验往往有一些茫然的感觉:不知从何处开始学起.作为一个 Linux系统管理员,我看了许多有关Linux的文档和书籍,并为学习 ...
