Lognormal distribution 对数正态分布

转载：https://blog.csdn.net/donggui8650/article/details/101556041

在概率论中，对数正态分布是一种连续概率分布，其随机变量的对数服从正态分布。

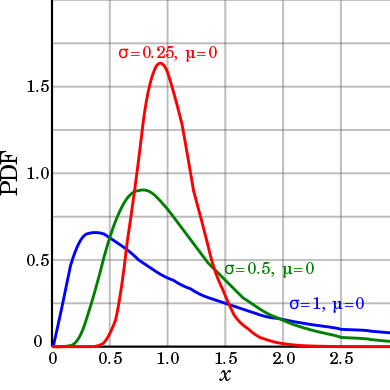
从统计学角度理解对数正态分布是这样的，在自然界有很多事物有增长速度很慢，甚至可以忽略不计（small percentage changes），但是其效果是对整个事物的影响，即每次增长都是对前面增长的乘积运算，但如果我们把他放入对数域，则可以放大他们的增长效果。

假设：x1,x2,...,xk表示第i个单位时间的单位增长率，则x1,x2,...xk大于等于0，令zi=log(xi)表示xi的对数，显然有：

因为x1,x2,...xk独立同分布，显然z1,z2...zk也是独立同分布，则根据中心极限定理（当样本量足够大时，样本均值的分布（变量和的分布）慢慢变成正态分布）有：