Acwing 843. n-皇后问题

n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

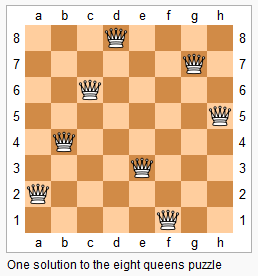
现在给定整数n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数n。

输出格式

每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。

其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

数据范围

1≤n≤91≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

第一种解法

思路:如上图,只需要判断列，左斜线(y = -x + b --> b = x + y)和右斜线(y = x + b--> b = y - x)三种情况，其中b(截距)就是我们的在格子的位置

 #include<iostream>

 using namespace std;

 const int N = ;
 int n;
 char g[N][N];
 bool col[N],dg[N],udg[N];

 void dfs(int y){
     if(n == y){
         for(int i = ;i < n;i++) puts(g[i]);
         puts("");
         return;
     }

     for(int i = ;i < n;i++){
         if(col[i] ==  && dg[n + y - i] ==  && udg[ y + i] == ){
             g[y][i] = 'Q';
             col[i] = dg[n + y - i] = udg[y  + i] = true;
             dfs(y + );
             g[y][i] = '.';
             col[i] = dg[n + y - i] = udg[y  + i] = false;
         }
     }

 }

 int main(){
     scanf("%d",&n);
     for(int i = ;i < n;i++)
         for(int j = ;j < n;j++)
             g[i][j] = '.';
         dfs();
         return ;
 }

第二种解法

思路:每一个格子有放还是不放两种情况，顺次判断，时间复杂度n^2

 //
 #include<iostream>

 using namespace std;

 const int N = ;
 int n;
 char g[N][N];
 bool row[N],col[N],dg[N],udg[N];

 void dfs(int x,int y,int s){
     if(y == n) y = ,x++;//如果出界就转回来

     if(x == n){//枚举到最后一行
         //这里有可能皇后不够
         if(s == n){//如果摆放的皇后等于n,说明找到了一组解
             for(int i = ;i < n;i++) printf("%s\n",g[i]);
             puts("");
         }
         return;
     }
     //枚举格子的两种选择
     //第一种是不放皇后
     dfs(x,y+,s);//直接递归到下一个格子就可以了

     //第二种是放皇后
         if(!row[x] && !col[y] && !dg[n + x - y] && !udg[x + y]){
             g[x][y] = 'Q';
             row[x] = col[y] = dg[n + x - y] = udg[x + y] = true;
             dfs(x,y + ,s + );
             row[x] = col[y] = dg[n + x - y] = udg[x + y] = false;
             g[x][y] = '.';
         }
 }

 int main(){
     scanf("%d",&n);
     for(int i = ;i < n;i++)
         for(int j = ;j < n;j++)
             g[i][j] = '.';
         dfs(,,);//从左上角开始搜索
         return ;
 }