c++实现单纯形法现行规划问题的求解

在本程序中默认该现行规划问题有最优解

针对此问题：

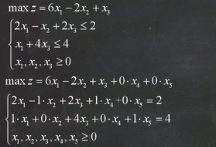
 #include<iostream>
 using namespace std;

 int check(float *sigema, int m) {
     for (int i = ; i <= m ; i++) {
         if (sigema[i] > ) {
             return ;
         }
     }
     return ;
 }

 //此程序已经化为标准型的线性规划问题中,且默认有最优解
 int main(int argc, char* argv[])
 {
     //数据输入部分
     int m, n;
     cout << "请输入变量个数：";
     cin >> m;
     cout << "请输入不等式个数:";
     cin >> n;
     float **matrix = new float*[n + ];      //系数矩阵
     for (int i = ; i <= n; i++) {
         matrix[i] = new float[m + ];
     }
     float *cj = new float[m + ];
     float *cB = new float[n + ];   //基变量系数
     int *XB = new int[n + ];   //用来标注基变量x的下标
     float *b = new float[n + ];
     float *sigema = new float[n + ];
     float *sita = new float[n + ];
     //初始化
     for (int i = ; i <= m; i++) {
         cj[i] = ;
     }
     for (int i = ; i <= n; i++) {
         cB[i] = ;
         XB[i] = ;
         b[i] = ;
         sigema[i] = ;
         sita[i] = ;
     }
     cout << "请输入目标函数系数(用空格间开)：" << endl;
     for (int i = ; i <= m; i++) {
         cin >> cj[i];
     }
     cout << "请输入各不等式的系数和常量(用空格间开)：" << endl;
     for (int i = ; i <= n; i++) {
         cout << "不等式" << i << ": ";
         for (int j = ; j <= m + ; j++) {
             cin >> matrix[i][j];
         }
     }
     cout << "请输入目标函数中基变量下标：" << endl;
     for (int i = ; i <= n; i++) {
         cin >> XB[i];
         cB[i] = cj[XB[i]];
         //常量
         b[i] = matrix[i][m + ];
     }

     //计算检验数
     for (int i = ; i <= m; i++) {
         sigema[i] = cj[i];
         for (int j = ; j <= n; j++) {
             sigema[i] -= cB[j] * matrix[j][i];
         }
     }

     while (check(sigema, m) == ) {
         //寻找入基变量
     float maxn = sigema[];
     int sigema_xindex = ;
     float sigema_xcoefficient = ;
     for (int i = ; i <= m; i++) {
         if (maxn <= sigema[i]) {
             maxn = sigema[i];
             sigema_xindex = i;
             sigema_xcoefficient = cj[i];
         }
     }
     //计算sita
     for (int i = ; i <= n; i++) {
         if (matrix[i][sigema_xindex] > ) {
             sita[i] = b[i] / matrix[i][sigema_xindex];
         }
         else {
             sita[i] = ; //表示sita值为负数
         }
     }
     //寻找出基变量
     float minn = sita[];
     int sita_xindex = ;
     for (int i = ; i <= n; i++) {
         if (minn >= sita[i] && sita[i] > ) {
             minn = sita[i];
             sita_xindex = i;
         }
     }
     //入基出基变换,先入基再出基
     //入基操作
     for (int i = ; i <= n; i++) {
         if (i == sita_xindex) {
             XB[i] = sigema_xindex;
             cB[i] = sigema_xcoefficient;
             break;
         }
     }
     //出基计算
     //化1
     //cout << endl << "此处为化1的结果------" << endl;
     float mul1 = matrix[sita_xindex][sigema_xindex];
     for (int i = ; i <= m; i++) {
         matrix[sita_xindex][i] /= mul1;
     }
     b[sita_xindex] /= mul1;
     //化0
     //cout << endl << "此处为化0的结果------" << endl;
     for (int i = ; i <= n; i++) {
         if (i == sita_xindex) {
             continue;
         }
         float mul2 = matrix[i][sigema_xindex] / matrix[sita_xindex][sigema_xindex];
         for (int j = ; j <= m; j++) {
             matrix[i][j] -= (matrix[sita_xindex][j] * mul2);
         }
         b[i] -= (b[sita_xindex] * mul2);
     }
     for (int i = ; i <= n; i++) {
         if (i == sita_xindex) {
             continue;
         }
     }
     for (int i = ; i <= m; i++) {
         sigema[i] = cj[i];
         for (int j = ; j <= n; j++) {
             sigema[i] -= cB[j] * matrix[j][i];
         }
     }
     }
     float MaxZ = ;
     float *result = new float[m + ];
     for (int i = ; i <= m; i++) {
         result[i] = ;
     }
     for (int i = ; i <= n; i++) {
         result[XB[i]] = b[i];
     }
     cout << "最优解为：X = (";
     for (int i = ; i < m; i++) {
         cout << result[i] << ",";
     }
     cout << result[m] << ")" << endl;
     for (int i = ; i <= m; i++) {
         MaxZ += result[i] * cj[i];
     }
     cout << "最优值为：MzxZ = " << MaxZ;
     return ;
 }

程序运行结果：