快速傅立叶变换&HDU 1402

参考http://www.cnblogs.com/v-July-v/archive/2011/08/13/2214132.html

《算导》

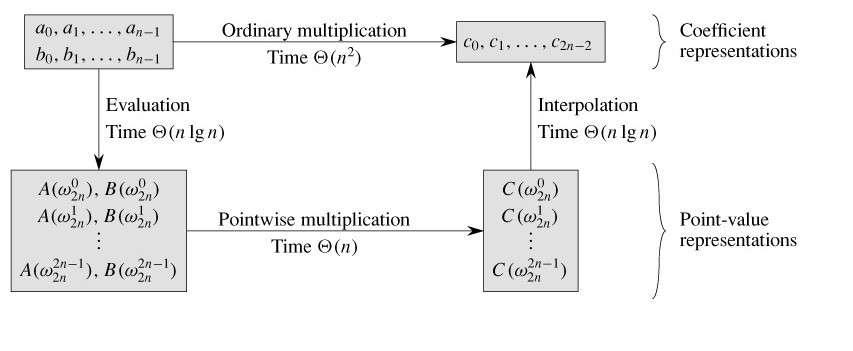
那么，更快速的多项式乘法就依赖于能否把一个系数形式的多项式快速转化成点值对的形式，和点值对形式快速转化成系数形式。即如下形式：

下图中的Evaluation + Pointwise multiplication + Interpolation 三个合过程。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>

using namespace std;
const int N = 500005;
const double PI = acos(-1.0);

struct Virt
{
    double r, i;

    Virt(double r = 0.0,double i = 0.0)
    {
        this->r = r;
        this->i = i;
    }

    Virt operator + (const Virt &x)
    {
        return Virt(r + x.r, i + x.i);
    }

    Virt operator - (const Virt &x)
    {
        return Virt(r - x.r, i - x.i);
    }

    Virt operator * (const Virt &x)
    {
        return Virt(r * x.r - i * x.i, i * x.r + r * x.i);
    }
};

//雷德算法--倒位序
void Rader(Virt F[], int len)
{
    int j = len >> 1;
    for(int i=1; i<len-1; i++)
    {
        if(i < j) swap(F[i], F[j]);
        int k = len >> 1;
        while(j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if(j < k) j += k;
    }
}

//FFT实现
void FFT(Virt F[], int len, int on)
{
    Rader(F, len);
    for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT
    {
        Virt wn(cos(-on*2*PI/h), sin(-on*2*PI/h));  //单位复根e^(2*PI/m)用欧拉公式展开
        for(int j=0; j<len; j+=h)
        {
            Virt w(1,0);            //旋转因子
            for(int k=j; k<j+h/2; k++)
            {
                Virt u = F[k];
                Virt t = w * F[k + h / 2];
                F[k] = u + t;     //蝴蝶合并操作
                F[k + h / 2] = u - t;
                w = w * wn;      //更新旋转因子
            }
        }
    }
    if(on == -1)
        for(int i=0; i<len; i++)
            F[i].r /= len;
}

//求卷积
void Conv(Virt a[],Virt b[],int len)
{
    FFT(a,len,1);
    FFT(b,len,1);
    for(int i=0; i<len; i++)
        a[i] = a[i]*b[i];
    FFT(a,len,-1);
}

char str1[N],str2[N];
Virt va[N],vb[N];
int result[N];
int len;

void Init(char str1[],char str2[])
{
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    len = 1;
    while(len < 2*len1 || len < 2*len2) len <<= 1;

    int i;
    for(i=0; i<len1; i++)
    {
        va[i].r = str1[len1-i-1] - '0';
        va[i].i = 0.0;
    }
    while(i < len)
    {
        va[i].r = va[i].i = 0.0;
        i++;
    }
    for(i=0; i<len2; i++)
    {
        vb[i].r = str2[len2-i-1] - '0';
        vb[i].i = 0.0;
    }
    while(i < len)
    {
        vb[i].r = vb[i].i = 0.0;
        i++;
    }
}

void Work()
{
    Conv(va,vb,len);
    for(int i=0; i<len; i++)
        result[i] = va[i].r+0.5;
}

void Export()
{
    for(int i=0; i<len; i++)
    {
        result[i+1] += result[i]/10;
        result[i] %= 10;
    }
    int high = 0;
    for(int i=len-1; i>=0; i--)
    {
        if(result[i])
        {
            high = i;
            break;
        }
    }
    for(int i=high; i>=0; i--)
        printf("%d",result[i]);
    puts("");
}

int main()
{
    while(~scanf("%s%s",str1,str2))
    {
        Init(str1,str2);
        Work();
        Export();
    }
    return 0;
}