Fibonacci series(斐波纳契数列)的几种常见实现方式

费波那契数列的定义：

费波那契数列（意大利语：Successione
di Fibonacci），又译费波拿契数、斐波那契数列、斐波那契数列、黄金切割数列。

在数学上，费波那契数列是以递归的方法来定义：

• 
• 
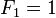
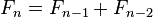• (n≧2)

用文字来说，就是费波那契数列由0和1開始。之后的费波那契系数就由之前的两数相加。

首几个费波那契系数是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

特别指出：0不是第一项。而是第零项。

以下是费波那契数列的几种常见编程实现：

1、常规实现：

int Fibonacci(int n)
{
	int a = 1, b = 1;
	if(n < 0)
	{
		printf("The fibonacci number exists only with nonnegative index.\n");
		return -1;
	}
	else if (n == 0)
		return 0;
	else if(n==1 || n==2)
		return 1;
	else
	{
		for(int i=3; i<=n; i++)
		{
			int tmp = b;
			b = a + b;
			a = tmp;
		}
		return b;
	}
}

2、递归实现：

int Fibonacci(int n)
{
	if(n < 0)
		printf("The fibonacci number exists only with nonnegative index.\n");
	else
	{
		if(n == 0)
			return 0;
		else if(n == 1)
			return 1;
		else
			return Fibonacci(n - 1) + Fibonacci(n - 2);
	}
}

3、迭代实现：

int Fibonacci_iter(int a, int b, int count)
{
	if(count < 0)
		printf("The fibonacci number exists only with nonnegative index.\n");
	else if(count == 0)
		return b;
	else
		return Fibonacci_iter(a + b, a, count - 1);
}

int Fibonacci(int n)
{
	return Fibonacci_iter(1, 0, n);
}

4、元编程实现：

#include<iostream>

using namespace std;

int Result;

//主模板
template<int N> //模板
class Fibonacci
{
public:
	enum{Result = Fibonacci<N-1>::Result + Fibonacci<N-2>::Result };   //枚举。带有隐含计算
};

//全然特化模板
template<>
class Fibonacci<1> //带常參数1的构造函数
{
public:
	enum { Result = 1 };   //给枚举赋初值1
};

//全然特化模板
template<>
class Fibonacci<0> //带參数0的模板
{
public:
	enum { Result = 0 };   //给枚举赋初值0
};

int main()
{
	std::cout << "第20项的Fibonacci数是：" << Fibonacci<20>::Result << std::endl;   //隐含计算
	system("pause");
	return 1;
}

总结：

递归（英语：Recursion）。又译为递回，在数学与计算机科学中。是指在函数的定义中使用函数自身的方法。

迭代，数学中的迭代能够指函数迭代的过程。即重复地运用同一函数计算，前一次迭代得到的结果被用于作为下一次迭代的输入。

使用递归要注意的有两点:

1)递归就是在过程或函数里面调用自身;

2)在使用递归时,必须有一个明白的递归结束条件,称为递归出口.

递归分为两个阶段:

1)递推:把复杂的问题的求解推到比原问题简单一些的问题的求解;

2)回归:当获得最简单的情况后,逐步返回,依次得到复杂的解.

迭代:利用变量的原值推算出变量的一个新值.假设递归是自己调用自己的话,迭代就是A不停的调用B.

递归中一定有迭代,可是迭代中不一定有递归,大部分能够相互转换.能用迭代的不用递归,递归调用函数,浪费空间,而且递归太深easy造成堆栈的溢出.

元编程（Metaprogramming）是指某类计算机程序的编写。这类计算机程序编写或者操纵其它程序（或者自身）作为它们的数据，或者在执行时完毕部分本应在编译时完毕的工作。非常多情况下比手工编写所有代码相比工作效率更高。编写元程序的语言称之为元语言。被操作的语言称之为目标语言。一门语言同一时候也是自身的元语言的能力称之为反射。

參考文献：

费波那契数列：http://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97

迭代：http://zh.wikipedia.org/wiki/%E8%BF%AD%E4%BB%A3

递归：http://zh.wikipedia.org/wiki/%E9%80%92%E5%BD%92

递归与迭代的差别：http://blog.csdn.net/swliao/article/details/5337896

递归与迭代：http://blog.csdn.net/ljyf5593/article/details/5935795

关于fibonacci递归算法和迭代算法在C和Scheme下实现存在差距的疑惑：http://bbs.csdn.net/topics/190008464