《学渣的电子技术自学笔记》——三极管的放大区、截止区与饱和区(基于NPN型）

《学渣的电子技术自学笔记》——三极管的放大区、截止区与饱和区(基于NPN型）

1.放大区

  三极管输出特性曲线近似水平的部分是放大区。在放大区，\(I_C=\overline{β}I_B\)。因此,放大区也被称作线性区。三极管处于放大状态时，发射结正向偏置，集电结反向偏置。对NPN型而言，\(U_{CE}＞U_{BE},U_{BE}＞0，U_{BC}＜0\)。
 

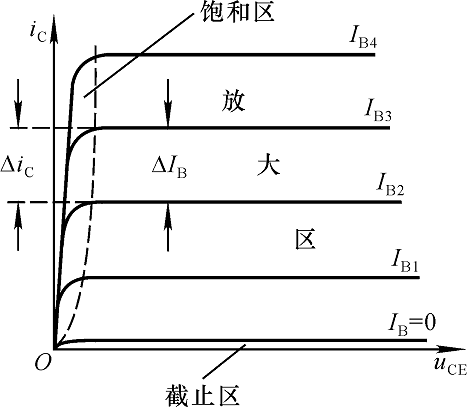
三极管输出特性曲线

 

2.截止区

  \(I_B=0\)的曲线以下的区域处于截止区。此时发射结处于反偏，集电结依然是反偏。对于NPN型而言，\(U_{BE}≤0\)（对于NPN型硅管而言，\(U{BE}＜0.5\)时已经开始截止，但为了截止可靠，常使\(U_{BE}≤0\)）。此时，\(I_C≈0，U_{CE}≈U_{CC}\)。

3.饱和区

  集电结正偏、发射结正偏时，三极管处于饱和状态。\(I_B\)对\(I_C\)的影响较小，两者不成正比。此时\(U_{CE}≈0，I_C≈{U_{CC}\over{R_C}}\)。

关于截止区和饱和区的理解
  \(I_B\)其实就像是水流的闸门控制信号，当控制信号为0时，闸门关闭，受其控制的\(I_C\)便被截断。
  在放大区，\(I_C=\overline{β}I_B\)。但\(U_{CE}=U_{CC}-\overline{β}I_BR_C\)，随着\(I_B\)不断增大，\(U_{CE}\)不断减小，直至\(U_{CE}＜U_{BE}\)。此时，集电结正偏，三极管状态变为饱和。此时，对于CEO回路来说，三极管近似于导线，\(U_{CE}≈0，I_C≈{U_{CC}\over{R_C}}\)。

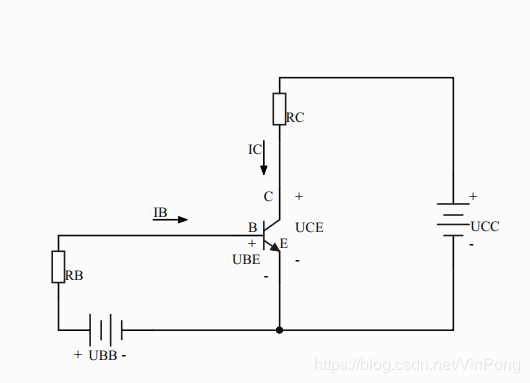
NPN型三极管共发射极电路