可落地的DDD(3)-如何利用DDD进行微服务的划分

摘要

前面两篇介绍了DDD的目标管理、DDD的工程结构调整。这篇讨论微服务的划分。微服务是目前后端比较流行的架构体系了，那么如何做好一个微服务的划分？一个微服务的粒度应该是多大呢？这篇主要介绍如何结合DDD进行领域划分。

工程结构代码

上篇介绍了可落地的DDD的(2)-为什么说MVC工程架构已经过时
很多朋友留言说，有没有sample code，要不然太湿了，不是很明白。这里写了个sample。

就以一个博客网站为例
page1:博客列表页： 展示所有用户发表的博客

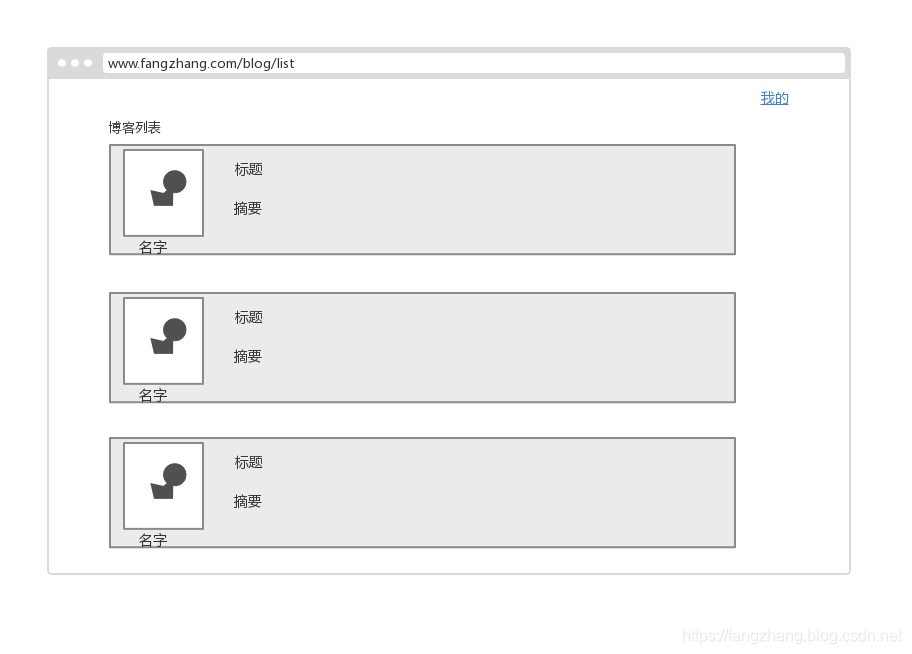
page2: 个人介绍页：有个人简介和博客列表

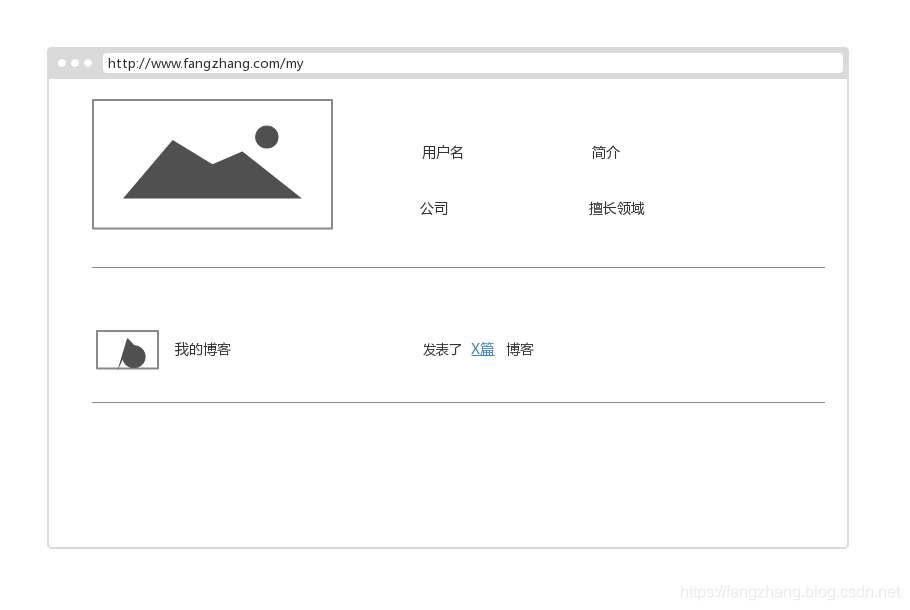
page3：博客详情页.

不同的业务展示的用户/博客的字段不一致

建模

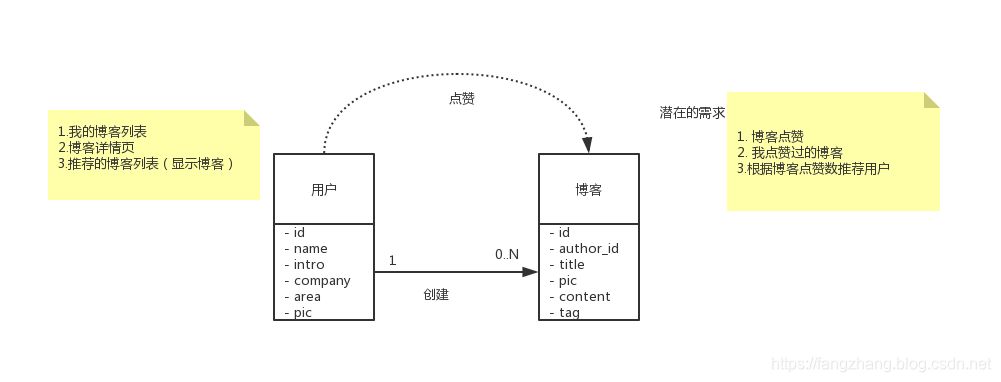
后期应该会有用户和博客交互的需求。这期只有用户创建博客这层关联关系。

MVC架构

使用mvc模式写出来的代码，就是一路到底。
具体代码见mvc-structure

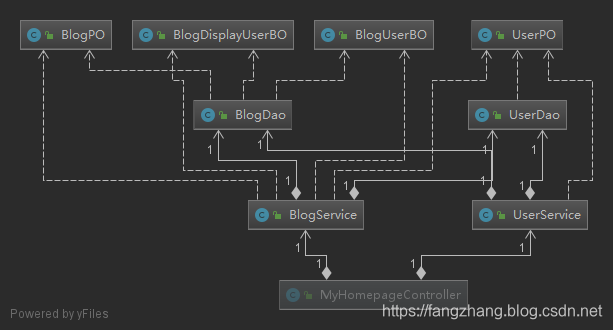
DDD

使用DDD写出来的工程结构就是，blog和user的交互只有一个地方，OpenXXXService
具体代码见DDD structure

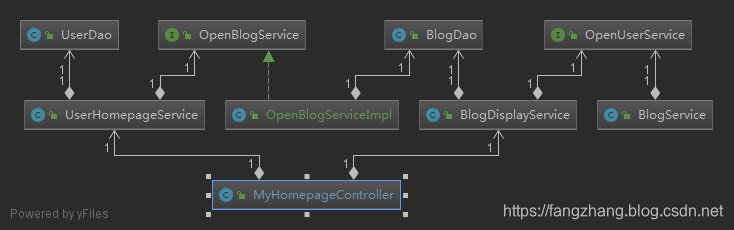
MVC VS DDD

从两张依赖图可以看出，DDD的依赖图清晰了，user和blog这两个领域之间的交互变的清晰了，user这个领域不用管blog领域发生了什么变更。只依赖OpenBlogService，而MVC模式呢，user和blog之间的交互太多了，如果再增加其他功能，这些模块之间就是够筹交错，理不清楚。

不同领域之间的交互多了，意味着一旦发生变更，需要修改逻辑了，那么需要修改的地方就是几何倍数的相关类。

比如业务发生了变更，统计【个人中心】的博客计数是用户已发表的文章。而这个已发表的可能随着业务的发展，包含多重含义

1. 用户写完了，对外开放了，
2. 运营审核通过
3. 博客未被软删除的。
   这些逻辑都会影响相关的查询，而这些逻辑的实现可能在数据库层面做，可能在redis中做，或者其他的方式。以MVC的写法，需要的需要修改的地方很多，以DDD的方式，不管这个逻辑怎么变，其他领域不需要知道，只有blog领域知道，只用更改blog领域的代码。

微服务划分

初版

确定了以DDD作为我们领域划分的指导原则后，我们首先按照领域对我们的业务进行了全面的分析，区分出哪些领域。然后按照如下标准进行了微服务的拆分

1. 一个领域一个服务的规则去拆分，
2. 同时为了保证领域的纯洁性，我们区分了领域服务，和前台服务。领域服务就是领域逻辑，不直接对前端暴露。前台服务组装各个领域服务，暴露给前端。
3. 同时为了保持扩展，我们预留了一个微服务作为服务孵化器。对于领域不清晰的（比如大部分的新的业务），放在这个服务里面孵化，然后等领域足够大的时候再拆分出去。

如下图

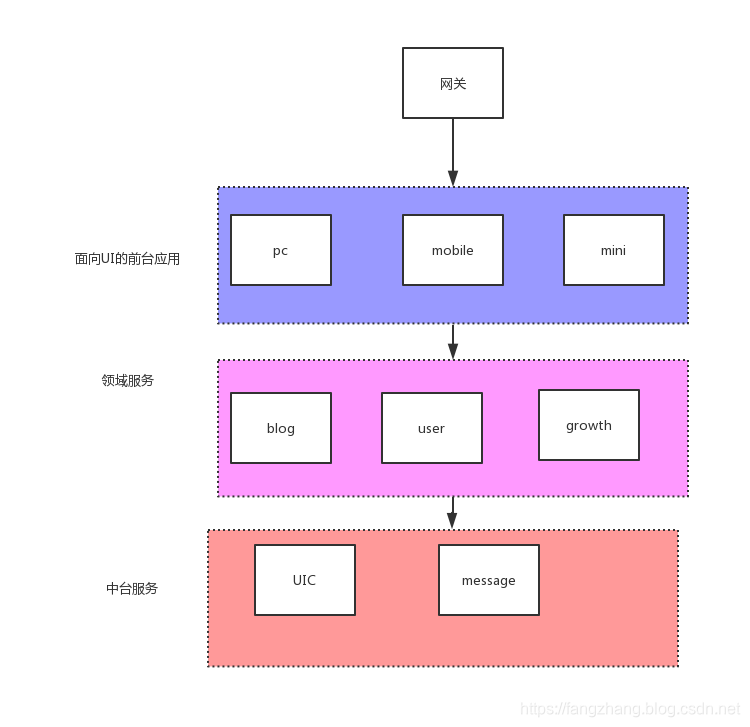
前台应用：
pc: pc端的页面展示
mobile: 移动端的页面展示
mini：小程序的页面展示

领域服务：
blog: 博客领域
user: 用户领域
growth: 领域孵化器

按照这样的标准去拆分后，一段时间后，很多问题暴露了。

• 服务热点问题
  我们是一个新的业务，在业务迭代的过程中，大部分新需求都是领域不清晰，不知道能不能迭代下去的。所以按照之前的标准，都往growth服务里面去写代码，这样导致几乎团队里面的所有的人都在开发这一个项目，失去了拆分微服务的意义。

• 服务依赖太严重
  无论写什么需求，都需要写多个应用，领域服务1个，前台如果有pc,需要在pc服务上开发，移动端要展示，要在mobile服务开发。服务之间的调用需要写rpc client接口，需要发版本，因为同时开发的人多，经常发生版本混乱，依赖问题。服务上线也很头疼，改一个小需求，需要部署多个服务。微服务一个很重要的点是去耦合，可独立部署。多了一层UI层作为微服务显然不是很合适。

• 领域划分有问题
  一个领域一个服务，粒度太小，有些东西不知道放在哪个服务里面，比如用户收藏博客，是放在用户服务里面，还是放在博客领域呢。

如何解决

不拆分单体应用不知道，一拆分问题一大堆。那么我们是怎么解决的呢？下期再见。

相关阅读
可落地的DDD(1)-目标讨论
可落地的DDD的(2)-为什么说MVC工程架构已经过时

关注【方丈的寺院】，第一时间收到文章的更新，与方丈一起开始技术修行之路