Problem 2 旅行计划 (travelling .cpp)———2019.10.6

lth tql,lzpclxf tql Orz

Problem 2 旅行计划 (travelling.cpp)
【题目描述】
小 Z 打算趁着暑假，开启他的旅行计划。但与其他同学不同的是，小 Z 旅
行时并不关心到达了哪个网红景点打了哪些卡。小 Z 更关注沿路的风光，而且
小 Z 觉得，尽管多次到达同一个地方，但如果来时的路不一样，也是别有一番
风味。
小 Z 事先准备了一份地图，地图上给出了 N 个小 Z 心仪的城市，依次编号
1…N，以及 M 条连接两个城市的路，编号 1…M。小 Z 打算把 M 条路都走一遍且
仅一遍，但他发现这样的路线可能是不存在的。于是他打算，当他走到一个城
市后发现从这个城市出发的道路他都已经走过了，他便会坐飞机到另一个城市，
然后继续他的旅行。
现在小 Z 想知道，在最好的路线计划下，他至少要坐多少趟飞机。
【输入格式】
第一行为测试数据组数 T（1≤T≤10） 。
每组测试数据的第一行为城市数 N 及道路数 M。
接下来 M 行，每行两个整数 x 和 y，表示一条连接城市 x 和城市 y 的双向
道路。
【输出格式】
对于每组测试数据，输出第一行包含一个整数 K，表示小 Z 至少要坐多少
趟飞机。
接下来 K+1 行，第 i 行输出小 Z 的第 i 段行程。若第 i 段行程经过 x 条道
路，则先输出 x，然后输出 x 个整数，分别表示路线经过的道路的编号。若是
正向通过第 i 条道路，则输出 i，否则输出-i。
若有多组方案，输出任意一组。
【样例输入】
1
3 3
1 2
1 3
2 3
【样例输出】
0
3 1 3 -2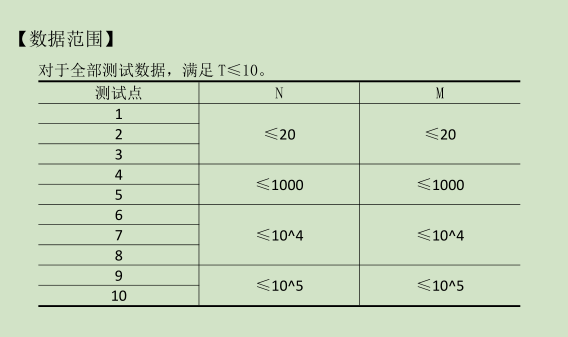

（复制不下来，就扣下来吧）

每个连通块显然是独立的。对于一个连通块（除了单个点的），如果奇度数点个数 为 k，

那么至少需要 max(k/2,1)条路径。这是因为在一个无向图中，将两个度数为奇数的

点连起来，就可以消去两个奇数点。所以如果一个无向图要有欧拉回路(全部点的度数全

为偶数)，只要加 k/2 条边就可以了。于是乎，我们只要将一个连通块变成欧拉图，搜一

遍得到路径，再将我们人为添加的边删掉，剩下的就是这个连通块的"笔画"了。 这里为

什么一定变成欧拉回路而不是欧拉通路，其实这里欧拉回路和欧拉通路都是 可以的，得

到的答案是一样的。主要是算法实现上的问题，如果变成欧拉通路，就一定得 从剩下的

两个奇数点出发，终止。至于为什么这里加 k/2 条边后扫出的结果删掉多加的边 就是答

案，并且这个答案=max(k/2,1)呢？这是因为一个图中，我们从奇数点开始走，停止 的也

一定是在奇数点，那么再一遍遍不重复地从图中走出一条条类似前面地路径(奇数点 开始

，奇数点结束)然后我们将这些路径地终点连接下一条路径的起点(多加的边)，这样又 因为

每一条路径的起止点都为奇数点，一条边删去两个奇数点。所以最终把他们连成欧拉 回路所需的边的数量就是 k/2。

 #include<iostream>
 #include<cstdio>
 #include<vector>
 #include<cstring>
 using namespace std;
 const int N=;
 vector<int> ans[N];
 int T,n,m,tot=,head[N],vis[N],in[N],cnt;
 struct node {
     int to,nex,flag,id;
 } a[N>>];
 inline int read() {//快读
     int x=,f=;
     char ch=getchar();
     while(ch<''||ch>'') {
         if(ch=='-')f=-;
         ch=getchar();
     }
     while(ch>=''&&ch<='')
         x=(x<<)+(x<<)+(ch^),ch=getchar();
     return x*f;
 }
 void add(int x,int y,int id) {//加边
     a[++tot].to=y;
     a[tot].nex=head[x];
     a[tot].flag=;
     a[tot].id=id;
     head[x]=tot;
 }
 void dfs(int x) {
     vis[x]=;
     for(int i=head[x]; i; i=a[i].nex) {
         int y=a[i].to,emm=a[i].flag;
         if(!emm) {
             a[i].flag=a[i^].flag=;
             dfs(y);
             if(a[i].id)ans[cnt].push_back(-a[i].id);
             else cnt++;
         }
     }
 }
 int main() {
     // freopen("travelling.in","r",stdin);
     // freopen("travelling.out","w",stdout);
     T=read();
     while(T--) {
         for(int i = ; i <= cnt; i ++) ans[i].clear();
         tot=,cnt=;
         memset(head,,sizeof(head));
         memset(vis,,sizeof(vis));
         memset(in,,sizeof(in));//多组数据注意清空数组
         n=read();
         m=read();
         for(int i=,x,y; i<=m; i++) {
             x=read();
             y=read();
             add(x,y,i);
             add(y,x,-i);
             in[x]++,in[y]++;
         }
         int now=;
         for(int i=; i<=n; i++)
             if(in[i]%==) {
                 if(now) {
                     add(i,now,);
                     add(now,i,);
                     now=;
                 } else now=i;
             }
         for(int i=; i<=n; i++)
             if(!vis[i]&&in[i]%) {
                 cnt++;
                 dfs(i);
                 cnt--;//回溯
             }
         for(int i=; i<=n; i++)
             if(!vis[i]&&in[i])
                 cnt++,dfs(i);
         //输出
         printf("%d\n",cnt - );
         for(int i=; i<=cnt; i++) {
             printf("%d ",ans[i].size());
             for(int j=; j<ans[i].size(); j++)
                 printf("%d ",ans[i][j]);
             printf("\n");
         }
         printf("\n");
     }
     // fclose(stdin);
     // fclose(stdout);
     return ;
 }