数据结构学习笔记05图(最小生成树 Prim Kruskal)

最小生成树Minimum Spanning Tree

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

　　树: 无回路

　  　　|V|个顶点，一定有|V|-1条边

　　生成树: 包含全部顶点

　　|V|-1 条边都在图里

　　边权重和最小

最小生成树存在<--->图联通

向生成树中任加一条边都一定构成回路

贪心算法

　　“贪”：每一步都要最好的

　　“好”：权重最小的边

　　需要约束：

　　　　①只能用图里有的边

　　　　②只能正好用掉|V|-1条边

　　　　③不能有回路

Prim算法— 让一棵小树长大

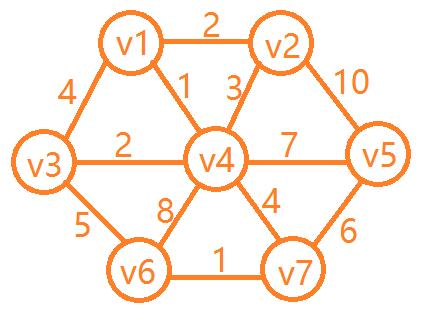
步骤
1	任意选取v1为顶点开始，并将v1收录进MST
2	v1有三条边，选取最短边(v1,v4)为1，并将v4收录进MST
3	MST={v1,v4}的边中在选取最小的(v1,v2)为2，将v2收录进MST
4	MST={v1,v4,v2}，选(v4,v3)为2，将v3收录进MST
5	不能选(v4,v2)3，会构成回路。所以接着选(v4,v7)4，将v7收录进MST
6	选(v7,v6)为1，将v6收录进MST
7	(v7,v5)6，将v7收录进MST

T = O(|V|^2) ---稠密图合算

 /* 邻接矩阵存储 - Prim最小生成树算法 */

 Vertex FindMinDist( MGraph Graph, WeightType dist[] )
 { /* 返回未被收录顶点中dist最小者 */
     Vertex MinV, V;
     WeightType MinDist = INFINITY;

     for (V=; V<Graph->Nv; V++) {
         if ( dist[V]!= && dist[V]<MinDist) {
             /* 若V未被收录，且dist[V]更小 */
             MinDist = dist[V]; /* 更新最小距离 */
             MinV = V; /* 更新对应顶点 */
         }
     }
     if (MinDist < INFINITY) /* 若找到最小dist */
         return MinV; /* 返回对应的顶点下标 */
     else return ERROR;  /* 若这样的顶点不存在，返回-1作为标记 */
 }

 /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
 int Prim( MGraph Graph, LGraph MST )
 {
     WeightType dist[MaxVertexNum], TotalWeight;
     Vertex parent[MaxVertexNum], V, W;
     int VCount;
     Edge E;

     /* 初始化。默认初始点下标是0 */
        for (V=; V<Graph->Nv; V++) {
         /* 这里假设若V到W没有直接的边，则Graph->G[V][W]定义为INFINITY */
            dist[V] = Graph->G[][V];
            parent[V] = ; /* 暂且定义所有顶点的父结点都是初始点0 */
     }
     TotalWeight = ; /* 初始化权重和     */
     VCount = ;      /* 初始化收录的顶点数 */
     /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
     MST = CreateGraph(Graph->Nv);
     E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */

     /* 将初始点0收录进MST */
     dist[] = ;
     VCount ++;
     parent[] = -; /* 当前树根是0 */

     while () {
         V = FindMinDist( Graph, dist );
         /* V = 未被收录顶点中dist最小者 */
         if ( V==ERROR ) /* 若这样的V不存在 */
             break;   /* 算法结束 */

         /* 将V及相应的边<parent[V], V>收录进MST */
         E->V1 = parent[V];
         E->V2 = V;
         E->Weight = dist[V];
         InsertEdge( MST, E );
         TotalWeight += dist[V];
         dist[V] = ;
         VCount++;

         for( W=; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
             if ( dist[W]!= && Graph->G[V][W]<INFINITY ) {
             /* 若W是V的邻接点并且未被收录 */
                 if ( Graph->G[V][W] < dist[W] ) {
                 /* 若收录V使得dist[W]变小 */
                     dist[W] = Graph->G[V][W]; /* 更新dist[W] */
                     parent[W] = V; /* 更新树 */
                 }
             }
     } /* while结束*/
     if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
        TotalWeight = ERROR;
     return TotalWeight;   /* 算法执行完毕，返回最小权重和或错误标记 */
 }

Kruskal算法— 将森林合并成树

步骤
1	选取一条最小边(v1,v4)为1
2	选取一条最小边(v6,v7)为1
3	选取一条最小边(v1,v2)为2
4	选取一条最小边(v3,v4)为2
5	不能选取最小边(v2,v4)3会构成回路
6	选取一条最小边(v7,v4)为4
7	选取一条最小边(v5,v7)为6

T= O(|E|log|E|)

 /* 邻接表存储 - Kruskal最小生成树算法 */

 /*-------------------- 顶点并查集定义 --------------------*/
 typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
 typedef Vertex SetName;     /* 默认用根结点的下标作为集合名称 */
 typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */

 void InitializeVSet( SetType S, int N )
 { /* 初始化并查集 */
     ElementType X;

     for ( X=; X<N; X++ ) S[X] = -;
 }

 void Union( SetType S, SetName Root1, SetName Root2 )
 { /* 这里默认Root1和Root2是不同集合的根结点 */
     /* 保证小集合并入大集合 */
     if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
         S[Root2] += S[Root1];     /* 集合1并入集合2  */
         S[Root1] = Root2;
     }
     else {                         /* 如果集合1比较大 */
         S[Root1] += S[Root2];     /* 集合2并入集合1  */
         S[Root2] = Root1;
     }
 }

 SetName Find( SetType S, ElementType X )
 { /* 默认集合元素全部初始化为-1 */
     if ( S[X] <  ) /* 找到集合的根 */
         return X;
     else
         return S[X] = Find( S, S[X] ); /* 路径压缩 */
 }

 bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
 { /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
     Vertex Root1, Root2;

     Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
     Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */

     if( Root1==Root2 ) /* 若V1和V2已经连通，则该边不能要 */
         return false;
     else { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
         Union( VSet, Root1, Root2 );
         return true;
     }
 }
 /*-------------------- 并查集定义结束 --------------------*/

 /*-------------------- 边的最小堆定义 --------------------*/
 void PercDown( Edge ESet, int p, int N )
 { /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
   /* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
     int Parent, Child;
     struct ENode X;

     X = ESet[p]; /* 取出根结点存放的值 */
     for( Parent=p; (Parent*+)<N; Parent=Child ) {
         Child = Parent *  + ;
         if( (Child!=N-) && (ESet[Child].Weight>ESet[Child+].Weight) )
             Child++;  /* Child指向左右子结点的较小者 */
         if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
         else  /* 下滤X */
             ESet[Parent] = ESet[Child];
     }
     ESet[Parent] = X;
 }

 void InitializeESet( LGraph Graph, Edge ESet )
 { /* 将图的边存入数组ESet，并且初始化为最小堆 */
     Vertex V;
     PtrToAdjVNode W;
     int ECount;

     /* 将图的边存入数组ESet */
     ECount = ;
     for ( V=; V<Graph->Nv; V++ )
         for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
             if ( V < W->AdjV ) { /* 避免重复录入无向图的边，只收V1<V2的边 */
                 ESet[ECount].V1 = V;
                 ESet[ECount].V2 = W->AdjV;
                 ESet[ECount++].Weight = W->Weight;
             }
     /* 初始化为最小堆 */
     for ( ECount=Graph->Ne/; ECount>=; ECount-- )
         PercDown( ESet, ECount, Graph->Ne );
 }

 int GetEdge( Edge ESet, int CurrentSize )
 { /* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */

     /* 将最小边与当前堆的最后一个位置的边交换 */
     Swap( &ESet[], &ESet[CurrentSize-]);
     /* 将剩下的边继续调整成最小堆 */
     PercDown( ESet, , CurrentSize- );

     return CurrentSize-; /* 返回最小边所在位置 */
 }
 /*-------------------- 最小堆定义结束 --------------------*/

 int Kruskal( LGraph Graph, LGraph MST )
 { /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
     WeightType TotalWeight;
     int ECount, NextEdge;
     SetType VSet; /* 顶点数组 */
     Edge ESet;    /* 边数组 */

     InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
     ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
     InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
     /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
     MST = CreateGraph(Graph->Nv);
     TotalWeight = ; /* 初始化权重和     */
     ECount = ;      /* 初始化收录的边数 */

     NextEdge = Graph->Ne; /* 原始边集的规模 */
     while ( ECount < Graph->Nv- ) {  /* 当收集的边不足以构成树时 */
         NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
         if (NextEdge < ) /* 边集已空 */
             break;
         /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
         if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
             /* 将该边插入MST */
             InsertEdge( MST, ESet+NextEdge );
             TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
             ECount++; /* 生成树中边数加1 */
         }
     }
     if ( ECount < Graph->Nv- )
         TotalWeight = -; /* 设置错误标记，表示生成树不存在 */

     return TotalWeight;
 }