Poj(2784)，二进制枚举最小生成树

题目链接：http://poj.org/problem?id=2784

Buy or Build

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1528		Accepted: 592

Description

World Wide Networks (WWN) is a leading company that operates large telecommunication networks. WWN would like to setup a new network in Borduria, a nice country that recently managed to get rid of its military dictator Kurvi-Tasch and which is now seeking for investments of international companies (for a complete description of Borduria, have a look to the following Tintin albums ``King Ottokar's Sceptre", ``The Calculus Affair" and ``Tintin and the Picaros"). You are requested to help WWN todecide how to setup its network for a minimal total cost.
Problem

There are several local companies running small networks (called
subnetworks in the following) that partially cover the n largest cities
of Borduria. WWN would like to setup a network that connects all n
cities. To achieve this, it can either build edges between cities from
scratch or it can buy one or several subnetworks from local companies.
You are requested to help WWN to decide how to setup its network for a
minimal total cost.

• All n cities are located by their two-dimensional Cartesian coordinates.
• There are q existing subnetworks. If q>=1 then each
  subnetwork c ( 1<=c<=q ) is defined by a set of interconnected
  cities (the exact shape of a subnetwork is not relevant to our problem).
• A subnetwork c can be bought for a total cost wc and it cannot be split (i.e., the network cannot be fractioned).
• To connect two cities that are not connected through the
  subnetworks bought, WWN has to build an edge whose cost is exactly the
  square of the Euclidean distance between the cities.

You have to decide which existing networks you buy and which edges
you setup so that the total cost is minimal. Note that the number of
existing networks is always very small (typically smaller than 8).

A 115 Cities Instance

Consider a 115 cities instance of the problem with 4 subnetworks
(the 4 first graphs in Figure 1). As mentioned earlier the exact shape
of a subnetwork is not relevant still, to keep figures easy to read, we
have assumed an arbitrary tree like structure for each subnetworks. The
bottom network in Figure 1 corresponds to the solution in which the
first and the third networks have been bought. Thin edges correspond to
edges build from scratch while thick edges are those from one of the
initial networks.

Input

The
first line contains the number n of cities in the country (
1<=n<=1000 ) followed by the number q of existing subnetworks (
0<=q<=8 ). Cities are identified by a unique integer value ranging
from 1 to n . The first line is followed by q lines (one per
subnetwork), all of them following the same pattern: The first integer
is the number of cities in the subnetwork. The second integer is the the
cost of the subnetwork (not greater than 2 x 10⁶ ). The
remaining integers on the line (as many as the number of cities in the
subnetwork) are the identifiers of the cities in the subnetwork. The
last part of the file contains n lines that provide the coordinates of
the cities (city 1 on the first line, city 2 on the second one, etc).
Each line is made of 2 integer values (ranging from 0 to 3000)
corresponding to the integer coordinates of the city.

Output

Your program has to write the optimal total cost to interconnect all cities.

Sample Input

7 3
2 4 1 2
3 3 3 6 7
3 9 2 4 5
0 2
4 0
2 0
4 2
1 3
0 5
4 4

Sample Output

17

Hint

Sample Explanation: The above instance is shown in Figure 2. An optimal solution is described in Figure 3 (thick edges come from an existing network while thin edges have been setup from scratch).




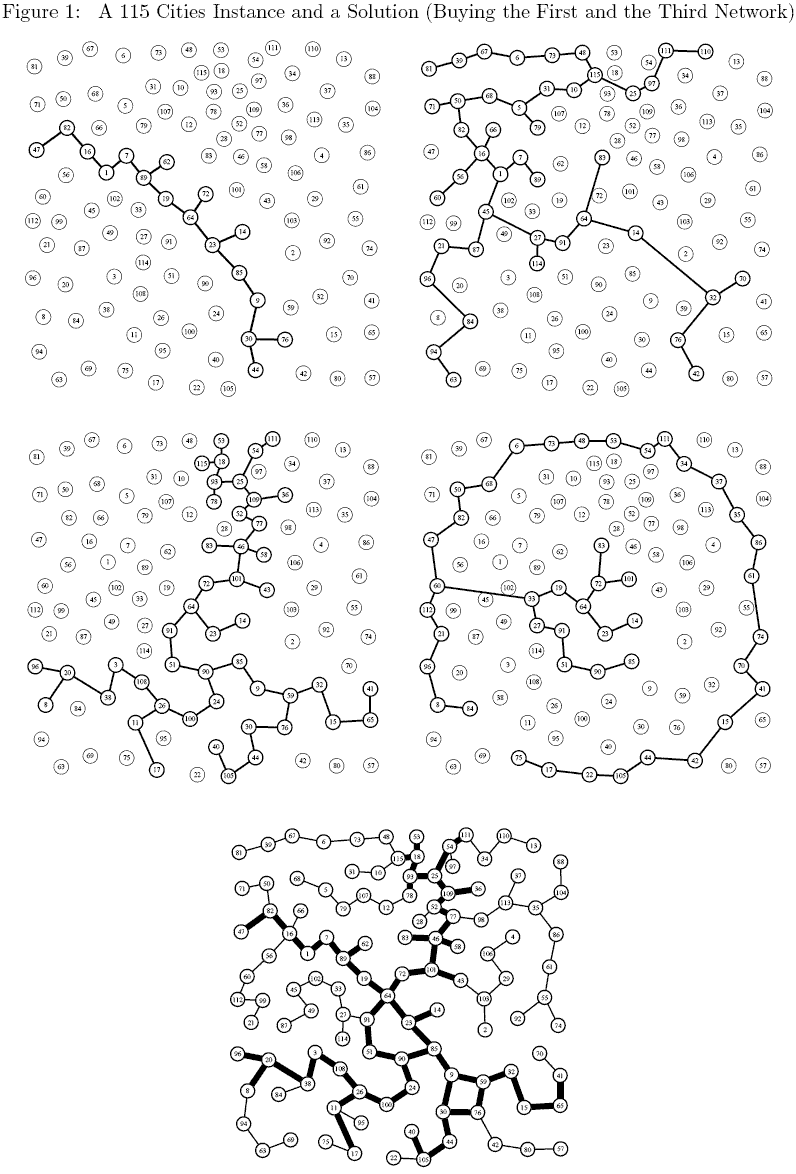
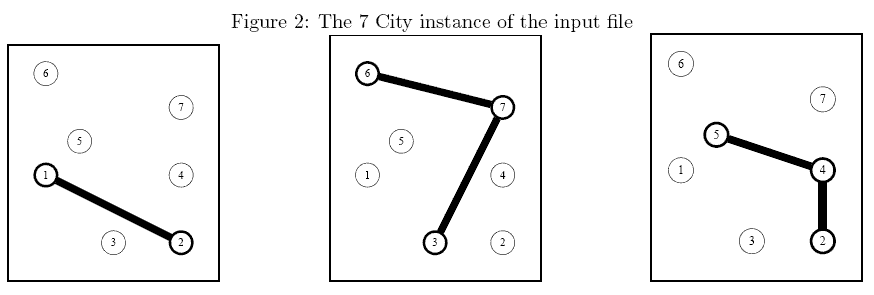
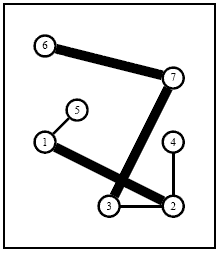
Figure 3: An optimal solution of the 7 City instance in which which
the first and second existing networkshave been bought while two extra
edges (1, 5) and (2, 4)

Source

Southwestern Europe 2005

 

分析：

这一个题目学到很多新知识。

1、最小生成树，权值为0时，有两种方法，一个是权值直接赋为0，也可以直接合并。

2、二进制枚举:

mark从000000000~111111111等等中枚举，但是怎么查看每一位是否是0呢？我就从第一个背包开始查，mark&(1<<i)遍历一边，这样就把每一位都找了是否用了背包，记录背包的钱，再把背包中的点都连起来，这样做MST的时候就不会找这条边了。(这里让我出错的地方就是，每次换一种拿背包的时候，都要将根节点初始化)。

3、这里的背包用邻接表来存，好厉害啊！我是菜鸟。

#include <stdio.h>
#include <vector>
#include <algorithm>

using namespace std;

#define MAXN 1005

struct Edge
{
    int u,v;
    int w;
    bool operator < (const Edge a) const
    {
        return w<a.w;
    }
}edge[MAXN*MAXN];

int n,m,q;
vector<int> v[];
int cost[];
int lx[MAXN];
int ly[MAXN];
int father[MAXN];

int Find_Set (int x)
{
    if(x!=father[x])
        father[x] = Find_Set(father[x]);
    return father[x];
}

int MST()
{
    int ans = ;
    int k = ;
    for(int i=;i<m;i++)
    {
        int fx = Find_Set(edge[i].u);
        int fy = Find_Set(edge[i].v);
        if(fx!=fy)
        {
            father[fx] = fy;
            ans +=edge[i].w;
            k++;
        }
        if(k==n-) break;
    }
    return ans;
}

int main()
{
    scanf("%d%d",&n,&q);
    for(int i=; i<q; i++)
    {
        v[i].clear();
        int t;
        scanf("%d%d",&t,&cost[i]);
        for(int j=; j<t; j++)
        {
            int to;
            scanf("%d",&to);
            v[i].push_back(to);
        }
    }
    for(int i=; i<=n; i++)
        scanf("%d%d",&lx[i],&ly[i]);

    m = ;
    for(int i=; i<=n; i++)
        for(int j=i+; j<=n; j++)
        {
            edge[m].u = i;
            edge[m].v = j;
            edge[m++].w = (lx[i]-lx[j])*(lx[i]-lx[j])+(ly[i]-ly[j])*(ly[i]-ly[j]);
        }
    sort(edge,edge+m);

    for(int i=; i<=n; i++)
        father[i] = i;

    int ans = MST();
    //printf("%d\n",ans);

    for(int mark=; mark<(<<q); mark++)
    {
        for(int i=;i<=n;i++)
            father[i] = i;

        int c = ;
        for(int i=; i<q; i++)
        {
            if(mark&(<<i))
            {
                c+=cost[i];
                for(int k=;k<v[i].size();k++)
                {
                    int fx = Find_Set(v[i][k]);
                    int fy = Find_Set(v[i][]);
                    if(fx!=fy)
                        father[fy] = fx;
                }
            }
        }
        ans = min(ans,c+MST());
    }
    printf("%d\n",ans);
    return ;
}