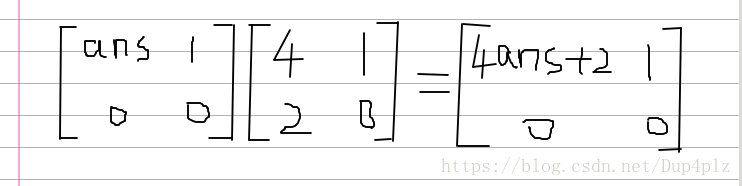HDU - 4990 Reading comprehension 【矩阵快速幂】
题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=4990
题意
初始的ans = 0
给出 n, m
for i in 1 -> n
如果 i 为奇数
ans = (ans * 2 + 1) % m
反之
ans = ans * 2 % m
思路
如果我们只计算 偶数项 那么递推公式就是
ans[n] = 4 * ans[n - 2] + 2
如果 n 是偶数 那么刚好 就按这个公式推 第 n / 2 项
如果 n 是奇数 那么就是 第 【 n / 2 项 】 * 2 + 1
可以推知的矩阵为
然后矩阵快速幂
AC代码
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>
#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back
using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;
const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const int maxn = 1e2 + 5;
//const int MOD = 1e4;
int MOD;
struct Matrix
{
ll a[2][2];
Matrix () {}
Matrix operator * (Matrix const &b)const
{
Matrix res;
CLR(res.a, 0);
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++)
for (int k = 0; k < 2; k++)
res.a[i][j] = (res.a[i][j] + this->a[i][k] * b.a[k][j]) % MOD;
return res;
}
};
Matrix pow_mod(Matrix base, int n)
{
Matrix ans;
CLR(ans.a, 0);
ans.a[0][1] = 1;
while (n > 0)
{
if (n & 1)
ans = ans * base;
base = base * base;
n >>= 1;
}
return ans;
}
int main()
{
Matrix base;
base.a[0][0] = 4;
base.a[0][1] = 0;
base.a[1][0] = 2;
base.a[1][1] = 1;
int n;
while (~scanf("%d%d", &n, &MOD))
{
Matrix ans = pow_mod(base, n / 2);
if (n & 1)
printf("%lld\n", (ans.a[0][0] * 2 + 1) % MOD);
else
printf("%lld\n", ans.a[0][0] % MOD);
}
}
HDU - 4990 Reading comprehension 【矩阵快速幂】的更多相关文章
- HDU 4990 Reading comprehension 矩阵快速幂
题意: 给出一个序列, \(f_n=\left\{\begin{matrix} 2f_{n-1}+1, n \, mod \, 2=1\\ 2f_{n-1}, n \, mod \, 2=0 \end ...
- hdu 4990 Reading comprehension 二分 + 快速幂
Description Read the program below carefully then answer the question. #pragma comment(linker, " ...
- hdu4990 Reading comprehension 矩阵快速幂
Read the program below carefully then answer the question.#pragma comment(linker, "/STACK:10240 ...
- HDU.1575 Tr A ( 矩阵快速幂)
HDU.1575 Tr A ( 矩阵快速幂) 点我挑战题目 题意分析 直接求矩阵A^K的结果,然后计算正对角线,即左上到右下对角线的和,结果模9973后输出即可. 由于此题矩阵直接给出的,题目比较裸. ...
- hdu 3117 Fibonacci Numbers 矩阵快速幂+公式
斐波那契数列后四位可以用快速幂取模(模10000)算出.前四位要用公式推 HDU 3117 Fibonacci Numbers(矩阵快速幂+公式) f(n)=(((1+√5)/2)^n+((1-√5) ...
- HDU 4990 Reading comprehension 简单矩阵快速幂
Problem Description Read the program below carefully then answer the question.#pragma comment(linker ...
- HDU 2842 (递推+矩阵快速幂)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2842 题目大意:棒子上套环.第i个环能拿下的条件是:第i-1个环在棒子上,前i-2个环不在棒子上.每个 ...
- hdu 2604 Queuing(矩阵快速幂乘法)
Problem Description Queues and Priority Queues are data structures which are known to most computer ...
- HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5950 Farmer John likes to play mathematics games with ...
随机推荐
- circular-array-loop(蛮难的)
https://leetcode.com/problems/circular-array-loop/ 题目蛮难的,有一些坑. 前后两个指针追赶找环的方法,基本可以归结为一种定式.可以多总结. pack ...
- 3747: [POI2015]Kinoman|线段树
枚举左区间线段树维护最大值 #include<algorithm> #include<iostream> #include<cstdlib> #include< ...
- HDU 5402 Travelling Salesman Problem(多校9 模拟)
题目链接:pid=5402">http://acm.hdu.edu.cn/showproblem.php?pid=5402 题意:给出一个n×m的矩阵,位置(i.j)有一个非负权值. ...
- vim g s 替换区别
vim g s 替换区别 PS:一篇好文收藏备用,今天用它解决了一个大问题. 发信人: vale (浅谷), 信区: VIM标 题: global命令详解 发信站: 水木社区 (Fri Ju ...
- C# Color颜色对照表
Color命名空间 using System.Drawing; Color.AliceBlue 240,248,255 Color.LightSalmon 255,160,122 Color.Ant ...
- zerglurker的C语言教程007——代码运行的顺序
软件开发中.代码有三种基本运行顺序: 顺序运行 代码从入口開始一条一条运行.直到返回或者结束 循环运行 在设定条件后,代码反复运行某一个或多个部分,直到达到某些条件后终止 条件运行 代码会先推断某些条 ...
- vue2.X v-model 指令
1.v-model指令 <!DOCTYPE html> <html> <head> <title></title> <script s ...
- JSBridge深度剖析
概述 做过混合开发的人都知道Ionic和PhoneGap之类的框架,这些框架在web基础上包装一层Native.然后通过Bridge技术的js调用本地的库. 在讲JSBridge技术之前.我们来看一下 ...
- csdn开源夏令营-ospaf中期报告
1.背景 随着将中期的代码托管到CSDN的平台上,ospaf(开源项目成熟度分析工具)已经有了小小的雏形.当然还远远不够. 首先还是要感谢这次活动组织方CSDN,感觉挺有G ...
- TCP/IP详解 卷一(第四、五章 ARP、RARP)
数据链路如 以太网都有自己的寻址机制(MAC)地址,而IP层使用的是IP地址. 当一台主机把以太网数据发送定位于同一局域网上的另一台主机时,是根据MAC地址来确定目的接口的.设备驱动程序从不检查IP数 ...