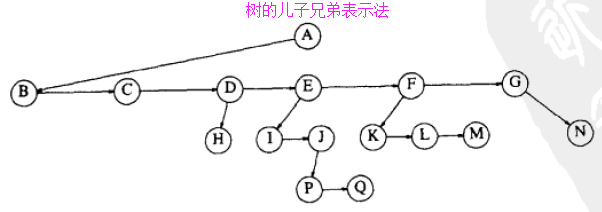
利用树的先序和后序遍历打印 os 中的目录树

【0】README

0.1）本代码均为原创，旨在将树的遍历应用一下下以加深印象而已；（回答了学习树的遍历到底有什么用的问题？）你对比下linux 中的文件树 和我的打印结果就明理了；

0.2）我们采用的是 儿子兄弟表示法 来 表示树的整体节点构造；

0.3）儿子兄弟表示法介绍

0.3.1）如下图所示： 向下的箭头（左指针）指向第一个儿子节点， 从左到右的箭头（右指针）指向下一个兄弟节点；（间接说明了树的节点有两个指针）

0.3.2）树节点定义代码如下：

struct Tree;
typedef struct Tree *Tree;

// we adopt child-sibling notation
struct Tree
{
    ElementType value;
    Tree firstChild;
    Tree nextSibling;
};

0.4）哥子第一次 使用这 丑到逼爆 的 编辑器，也是醉了，主要是markdown 对于源代码文件显示不够清晰， oh m g；

 

---

【1】任务来了

我们想要列出目录中所有文件的名字， 我们的输出格式将是：深度为 depth 的文件的名字将被 depth 次跳格缩进后打印出来；

---

【2】给出先序遍历+后序遍历目录树的实现代码

2.1）先序遍历步骤：

step1）访问根节点；

step2）先序遍历以儿子为根的子树；

step3）先序遍历以兄弟为根的子树；

download source code：https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter4/p68_preorder_common_tree.c

 

source code at a glance：

#include <stdio.h>
#include <malloc.h>

#define ElementType char
#define Error(str) printf("\n error: %s \n",str)   

struct Tree;
typedef struct Tree *Tree;

Tree createTree();
Tree makeEmpty(Tree t);
Tree insert(ElementType e, Tree t);

// we adopt child-sibling notation
struct Tree
{
    ElementType value;
    Tree firstChild;
    Tree nextSibling;
};

// create a tree with root node
Tree createTree()
{
    Tree t;

    t = (Tree)malloc(sizeof(struct Tree));
    if(!t) {
        Error("out of space, from func createTree");
        return NULL;
    }
    t->firstChild = NULL;
    t->nextSibling = NULL;
    t->value = '/';

    return t;
}

// make the tree empty
Tree makeEmpty(Tree t)
{
    if(t){
        makeEmpty(t->firstChild);
        makeEmpty(t->nextSibling);
        free(t);
    }
    return NULL;
}

//
Tree insert(ElementType e, Tree parent)
{
    Tree child;
    Tree newSibling;

    if(!parent){
        Error("for parent tree node is empty , you cannot insert one into the parent node, from func insert");
        return NULL;
    }

    newSibling = (Tree)malloc(sizeof(struct Tree));
    if(!newSibling) {
        Error("out of space, from func insert");
        return NULL;
    }
    newSibling->value = e;
    newSibling->nextSibling = NULL;
    newSibling->firstChild = NULL;// building the node with value e over

    child = parent->firstChild;
    if(!child) {
        parent->firstChild = newSibling;
        return parent;
    }

    while(child->nextSibling)
        child = child->nextSibling; // find the last child of parent node
    child->nextSibling = newSibling;

    return parent;
}

// find the tree root node with value equaling to e
Tree find(ElementType e, Tree root)
{
    Tree temp;

    if(root == NULL)
        return NULL;
    if(root->value == e)
        return root;

    temp = find(e, root->firstChild);
    if(temp)
        return temp;
    else
        return     find(e, root->nextSibling);
}

// analog print directories and files name in the tree, which involves preorder traversal.
void printPreorder(int depth, Tree root)
{
    int i;

    if(root) {
        for(i = ; i < depth; i++)
            printf("    ");
        printf("%c\n", root->value);
        printPreorder(depth + , root->firstChild);
        printPreorder(depth, root->nextSibling);
    }
}

int main()
{
    Tree tree;

    tree = createTree();

    printf("\n test for insert 'A' 'B' into the parent '/' and 'C' 'D' into the parent 'A' \n");
    insert('A', tree);
    insert('B', find('/', tree));
    insert('C', find('A', tree));
    insert('D', find('A', tree));
    printPreorder(, tree);

    printf("\n test for insert 'E' 'F' into the parent '/'  \n");
    insert('E', find('/', tree));
    insert('F', find('/', tree));
    printPreorder(, tree);

    printf("\n test for insert 'G' 'H' into the parent 'E' and 'I' into the parent 'H' and even 'J' 'K' into the parent 'I' \n");
    insert('G', find('E', tree));
    insert('H', find('E', tree));
    insert('I', find('H', tree));
    insert('J', find('I', tree));
    insert('K', find('I', tree));
    printPreorder(, tree);

    return ;
}

 

打印结果如下：

 

2.2）后序遍历步骤：（不同于二叉树的后序）

step1）后序遍历以儿子为根的子树； 

step2）访问根节点；

step3）后序遍历以兄弟为根的子树；

download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter4/p69_postorder_commone_tree.c

 

source code at a glance:

#include <stdio.h>
#include <malloc.h>

#define ElementType char
#define Error(str) printf("\n error: %s \n",str)   

struct Tree;
typedef struct Tree *Tree;

Tree createTree();
Tree makeEmpty(Tree t);
Tree insert(ElementType e, Tree t);

// we adopt child-sibling notation
struct Tree
{
    ElementType value;
    Tree firstChild;
    Tree nextSibling;
};

// create a tree with root node
Tree createTree()
{
    Tree t;

    t = (Tree)malloc(sizeof(struct Tree));
    if(!t) {
        Error("out of space, from func createTree");
        return NULL;
    }
    t->firstChild = NULL;
    t->nextSibling = NULL;
    t->value = '/';

    return t;
}

// make the tree empty
Tree makeEmpty(Tree t)
{
    if(t){
        makeEmpty(t->firstChild);
        makeEmpty(t->nextSibling);
        free(t);
    }
    return NULL;
}

//
Tree insert(ElementType e, Tree parent)
{
    Tree child;
    Tree newSibling;

    if(!parent){
        Error("for parent tree node is empty , you cannot insert one into the parent node, from func insert");
        return NULL;
    }

    newSibling = (Tree)malloc(sizeof(struct Tree));
    if(!newSibling) {
        Error("out of space, from func insert");
        return NULL;
    }
    newSibling->value = e;
    newSibling->nextSibling = NULL;
    newSibling->firstChild = NULL;// building the node with value e over

    child = parent->firstChild;
    if(!child) {
        parent->firstChild = newSibling;
        return parent;
    }

    while(child->nextSibling)
        child = child->nextSibling; // find the last child of parent node
    child->nextSibling = newSibling;

    return parent;
}

// find the tree root node with value equaling to e
Tree find(ElementType e, Tree root)
{
    Tree temp;

    if(root == NULL)
        return NULL;
    if(root->value == e)
        return root;

    temp = find(e, root->firstChild);
    if(temp)
        return temp;
    else
        return     find(e, root->nextSibling);
}

// analog print directories and files name in the tree, which involves postorder traversal.
void printPostorder(int depth, Tree root)
{
    int i;

    if(root) {
        printPostorder(depth + , root->firstChild);
        for(i = ; i < depth; i++)
            printf("    ");
        printf("%c\n", root->value);
        printPostorder(depth, root->nextSibling);
    }
}

int main()
{
    Tree tree;

    tree = createTree();
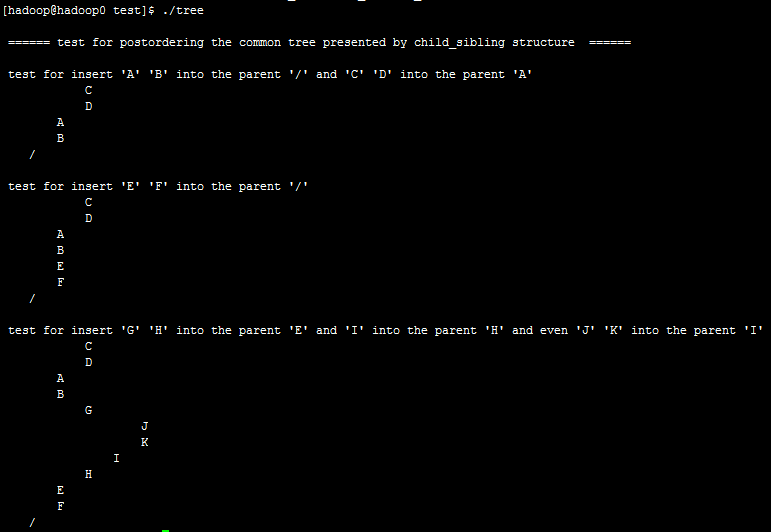
    printf("\n ====== test for postordering the common tree presented by child_sibling structure  ====== \n");    

    printf("\n test for insert 'A' 'B' into the parent '/' and 'C' 'D' into the parent 'A' \n");
    insert('A', tree);
    insert('B', find('/', tree));
    insert('C', find('A', tree));
    insert('D', find('A', tree));
    printPostorder(, tree);

    printf("\n test for insert 'E' 'F' into the parent '/'  \n");
    insert('E', find('/', tree));
    insert('F', find('/', tree));
    printPostorder(, tree);

    printf("\n test for insert 'G' 'H' into the parent 'E' and 'I' into the parent 'H' and even 'J' 'K' into the parent 'I' \n");
    insert('G', find('E', tree));
    insert('H', find('E', tree));
    insert('I', find('H', tree));
    insert('J', find('I', tree));
    insert('K', find('I', tree));
    printPostorder(, tree);

    return ;
} 

 

打印结果如下：