UVA1389 Hard Life[二分答案+最小割]

我真菜啊←地址

求最大密度子图方案。密度=边数/点数

---

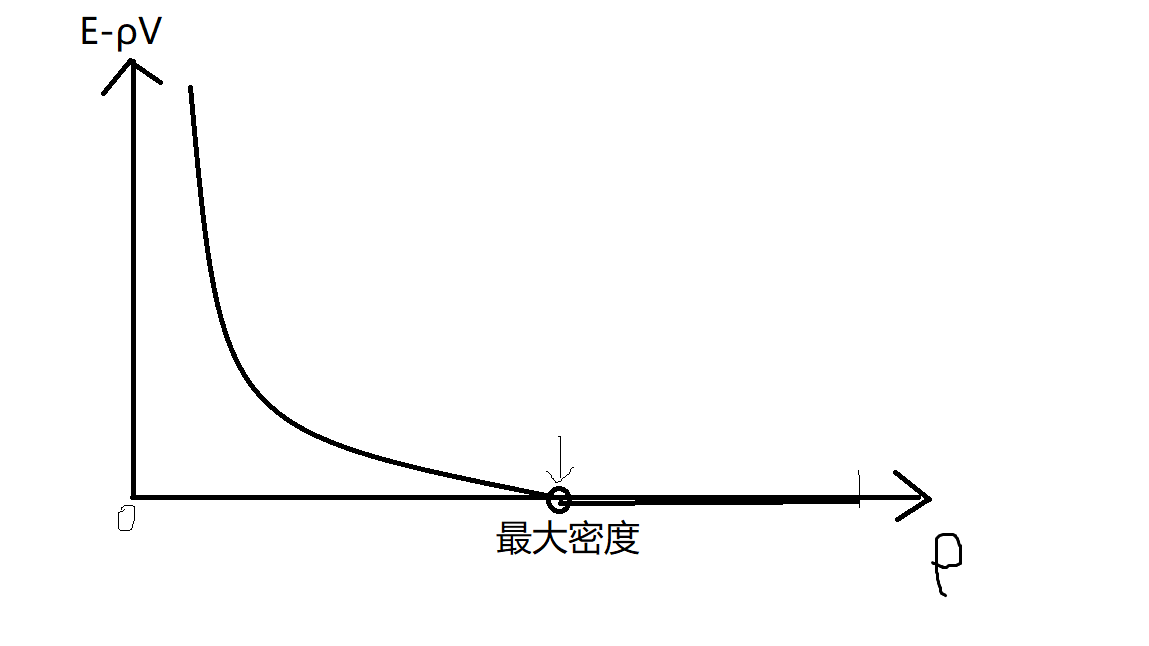
假设E,V为最大密度子图的边数点数。则$\forall \rho$有$\rho \leqslant \frac{E}{V}$即$E- \rho V \geqslant 0$,也就是说密度最大时不等式去等号，密度要是小一些的话就应大于0，那可以二分密度寻找最大的密度，判断是否合法的方法：要看左边的等式有没有大于0，那可以把点看成权值是$-\rho$的点，边抽象成权值为$1$的点，且其向连接两端的点连有向边。然后做最大权闭合子图，保证边选上就得把点也给选上。这样得到的最大权大于零说明密度枚举小了，而为零表示枚举值大于等于最大密度。那就通过二分找到那个刚好突变的数就是最大密度，这是停止二分把残量网络跑一遍，得所选点。

这题稍微卡精度，还是说我不太会写浮点数二分答案？很玄学。

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<queue>
 #include<cmath>
 using namespace std;
 typedef long long ll;
 typedef double db;
 #define dbg(x) cerr<<#x<<" = "<<x<<endl
 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,:;}
 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,:;}
 template<typename T>inline T _min(T A,T B){return A<B?A:B;}
 template<typename T>inline T _max(T A,T B){return A>B?A:B;}
 template<typename T>inline void inc(T&A,T B){A+=B;}
 inline int read(int&x){
     x=;int f=;char c;while(!isdigit(c=getchar()))if(c=='-')f=;
     while(isdigit(c))x=x*+c-'',c=getchar();if(c=='\n')return -;return f?-x:x;
 }
 const int N=+,M=+;const db eps=1e-,INF=99999999.0;
 int Head[N],cur[N],Next[M<<],v[M<<],dis[N],vis[N],tot,n,m,s,t;
 db w[M<<];
 inline void Addedge(int x,int y,db z){
     v[++tot]=y,Next[tot]=Head[x],Head[x]=tot,w[tot]=z;
     v[++tot]=x,Next[tot]=Head[y],Head[y]=tot,w[tot]=;
 }
 #define y v[j]
 inline int bfs(){
     queue<int> q;memset(dis,,sizeof dis),dis[s]=,q.push(s);
     for(register int i=;i<=(n+m)+;++i)cur[i]=Head[i];
     while(!q.empty()){
         int x=q.front();q.pop();
         for(register int j=Head[x];j;j=Next[j])if(w[j]>&&!dis[y]){
             dis[y]=dis[x]+,q.push(y);
             if(y==t)return ;
         }
     }
     return ;
 }
 db dinic(int x,db flow){
     if(flow<eps||x==t)return flow;
     db rest=flow,k;
     for(register int j=cur[x];j&&rest;cur[x]=j,j=Next[j])if(w[j]>&&dis[y]==dis[x]+){
         if((k=dinic(y,_min(rest,w[j])))<eps)dis[y]=;
         rest-=k,w[j]-=k,w[j^]+=k;
     }
     return flow-rest;
 }
 #undef y
 int flag,edge[][],cnt;
 db L,R,mid,res,maxflow,ans;

 inline db check(db rho){//dbg(rho);
     memset(Head,,sizeof Head);maxflow=ans=;tot=;
     for(register int i=;i<=m;++i)ans+=1.0,Addedge(s,i,1.0),Addedge(i,edge[i][]+m,INF),Addedge(i,edge[i][]+m,INF);
     for(register int i=;i<=n;++i)Addedge(i+m,t,rho);
     while(bfs())maxflow+=dinic(s,INF);
     ans-=maxflow;//dbg(maxflow);dbg(ans);
     return ans;
 }
 void dfs(int x){//cerr<<x<<endl;
     vis[x]=;for(register int j=Head[x];j;j=Next[j]){
 //        dbg(v[j]),dbg(w[j]);
         if(w[j]>&&!vis[v[j]])dfs(v[j]);
     }
 }

 int main(){//freopen("tmp.in","r",stdin);//freopen("tmp.out","w",stdout);
     while(~scanf("%d%d",&n,&m)){
         if(flag)puts("");else flag=;
         if(m==){printf("1\n1\n");continue;}
         for(register int i=;i<=m;++i)read(edge[i][]),read(edge[i][]);
         L=,R=m/2.0;s=n+m+,t=s+;
         while(R-L>eps){//dbg(L),dbg(R);
             mid=(L+R)/2.0;db res=check(mid);
             if(res<eps)R=mid-eps;
             else L=mid;
         }
         check(L),memset(vis,,sizeof vis),dfs(s);cnt=;
         for(register int i=;i<=n;++i)if(vis[i+m])++cnt;
         printf("%d\n",cnt);
         for(register int i=;i<=n;++i)if(vis[i+m])printf("%d\n",i);
     }
     return ;
 }