机器学习--聚类系列--K-means算法

一、聚类

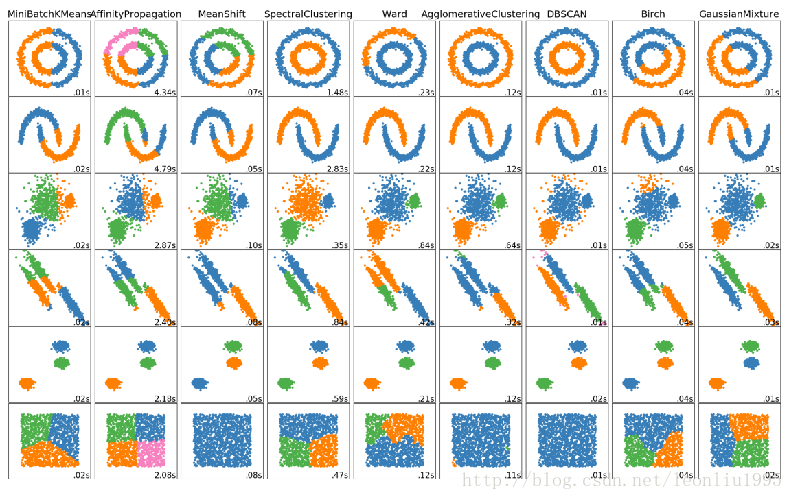
　　聚类分析是非监督学习的很重要的领域。所谓非监督学习，就是数据是没有类别标记的，算法要从对原始数据的探索中提取出一定的规律。而聚类分析就是试图将数据集中的样本划分为若干个不相交的子集，每个子集称为一个“簇”。它的难点是不好调参和评估。下面是sklearn中对各种聚类算法的比较。

　　

二、K-Means算法

　　KMeans算法在给定一个数k之后，能够将数据集分成k个“簇”={C1,C2,⋯,Ck}C={C1,C2,⋯,Ck}，不论这种分类是否合理，或者是否有意义。算法需要最小化平方误差：

　　　　　　　　　　　　　　　　　　

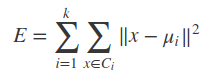
　　其中μi是簇Ci的均值向量，或者说是质心。其中‖x−μi‖^2代表每个样本点到均值点的距离（其实也是范数）。这里就稍微提一下距离度量。

　　所以要得到簇的个数,需要指定K值
　　质心：均值,即向量各维取平均即可
　　距离的度量：常用欧几里得距离和余弦相似度(先标准化)
　　优化目标:

　　　　　　

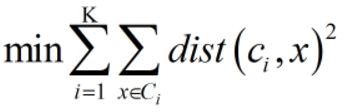
　　工作流程：

　　根据给定的K值，随便取K个点作为K个簇的质心，比如K=2，然后计算各个点到两个质心的距离，离哪个近则划入那一边，然后重新调整质心位置，再分簇，直至质心不再变动为止。

　　

　　优势：简单,快速,适合常规数据集
　　劣势:

• K值难确定，根本不知道有几个类
• 初值设置对结果影响很大，所以要多次取初值。有时候设置初始点，并不能正确分类。
• 复杂度与样本呈线性关系，样本越多计算越多
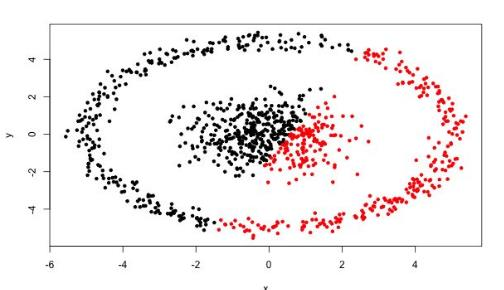
• 很难发现任意形状的簇，比如环状的，单计算到质心距离很难分类。