【数据结构与算法Python版学习笔记】递归(Recursion)——优化问题与策略

分治策略：解决问题的典型策略，分而治之

• 将问题分为若干更小规模的部分
• 通过解决每一个小规模部分问题，并将结果汇总得到原问题的解

递归算法与分治策略

• 递归三定律
• 体现了分支策略
• 应用相当广泛
  • 排序
  • 查找
  • 遍历
  • 求值等

---

优化问题

• 计算机科学中许多算法都是为了找到某些问题的最优解
  • 两点之间最短路径
  • 能最好匹配一系列点的直线
  • 满足一定条件的最小集合

经典案例：找零兑换

贪心策略

• 兑换最少个数的硬币
• 贪心策略及失效
  • 63=252+101+1*3
  • 63=21*3

递归解法

• 步骤
  • 确定基本结束条件
    
    需要兑换的找零，面值正好等于某种硬币
  • 减少问题规模
    
    对每种硬币尝试一次

• 低效代码

import time

def recMC(coinValueList, change):
    minCoins = change
    if change in coinValueList:
        return 1
    else:
        for i in [c for c in coinValueList if c <= change]:
            numCoins = 1+recMC(coinValueList, change-i)
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins

if __name__ == "__main__":
    print(time.clock())
    print(recMC([1, 5, 10, 25], 63))
    print(time.clock())

memoization 记忆化/函数值缓存

• 优化

  • 消除重复计算
    
    用一个表将计算过的中间结果保存起来，在计算之前查表看看是否已经计算过
    • 有，直接返回最优解
    • 无，进行递归调用

  import time
  def recMC(coinValueList, change, knowResults):
      minCoins = change
      if change in coinValueList:
          knowResults[change] = 1
          return 1
      elif knowResults[change] > 0:
          return knowResults[change]
      else:
          for i in [c for c in coinValueList if c <= change]:
              numCoins = 1+recMC(coinValueList, change-i, knowResults)
              if numCoins < minCoins:
                  minCoins = numCoins
                  knowResults[change] = minCoins
      return minCoins
  
  if __name__ == "__main__":
      meno = [0]*64
      print(time.clock())
      print(recMC([1, 5, 10, 25], 63, meno))
      print(time.clock())
      print(meno)
  
  >>>
  2e-07
  6
  0.0061154
  [0, 1, 0, 0, 0, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 2, 3, 4, 5, 6, 3, 4, 5, 6, 7, 3, 4, 5, 6, 7, 2, 3, 4, 5, 6, 3, 4, 5, 6, 7, 3, 4, 5, 6]
  

动态规划解法

• 步骤

  • 从最简单的“1分钱找零”的最优解开始，逐步狄加上去，直到我们需要的找零钱数
  • 在找零递加的过程中，一直加到求解找零钱数，自然得到最优解
  • 递加的过程能保持最优解的关键是，其依赖于更少钱数最优解的简单计算，而更少钱数的最优解已经得到了
  • 问题的最优解包含了更小规模子问题的最优解。
    
    这是一个最优化问题能够用动态规划策略解决的必要条件

• 思想

  • 从最简单的情况开始到达所需找零的循环
  • 每一步都依靠以前的最优解来得到本步骤的最优解，直到得到答案

• 代码实现

def dpMakeChange(coinValueList, change, minCoins, coinUsed):
    # 1.从一分钱到change逐个计算最少硬币数
    for cents in range(1, change+1):
        coinCounts = cents
        newCoin = 1
        # 2.减去每个硬币，向后查最少硬币数，同时记录总的最少数
        for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents-j]+1 < coinCounts:
                coinCounts = minCoins[cents-j]+1
                newCoin = j
        # 3.得到当前最少硬币数，记录到表中
        minCoins[cents] = coinCounts
        coinUsed[cents] = newCoin

    return minCoins[change]

def printCoins(coinUsed, change):
    coin = change
    while coin > 0:
        thisCoin = coinUsed[coin]
        print(thisCoin)
        coin = coin-thisCoin

if __name__ == "__main__":
    amnt=63
    clist=[1, 5, 10, 21, 25]
    coinUsed=[0]*(amnt+1)
    coinCount=[0]*(amnt+1)
    print("Making change for",amnt,"require",dpMakeChange(clist, amnt, coinCount,coinUsed),"coins")
    print("They are:")
    printCoins(coinUsed, amnt)
    print("The used list is as follows:")
    print(coinUsed)

>>>
Making change for 63 require 3 coins
They are:
21
21
21
The used list is as follows:
[0, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 21, 1, 1, 1, 25, 1, 1, 1, 1, 5, 10, 1, 1, 1, 10, 1, 1, 1, 1, 5, 10, 21, 1, 1, 10, 21, 1, 1, 1, 25, 1, 10, 1, 1, 5, 10, 1, 1, 1, 10, 1, 10, 21]

博物馆大盗问题

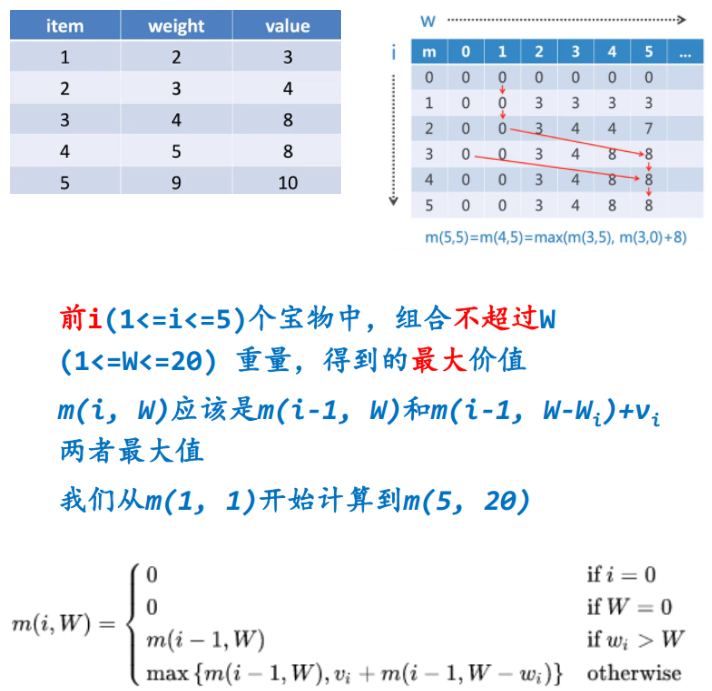
• 动态规范代码

def calcTreasure1():
    """动态规划宝物价值最大化"""
    # 宝物价值和重量
    tr = [
        None,
        {'w': 2, 'v': 3},
        {'w': 3, 'v': 4},
        {'w': 4, 'v': 8},
        {'w': 5, 'v': 8},
        {'w': 9, 'v': 10}
    ]

    # 达到最大承重
    max_w = 20

    # 初始化二位表格m[(i,w)]
    # 表示前i个宝物中，最大重量w的组合，所得到的最大价值
    # 当i什么都不取，或w上限为0，价值均为0
    m = {(i, w): 0 for i in range(len(tr))
                    for w in range(max_w+1)}
    #逐个填写二维表格
    for i in range(1,len(tr)):
        for w in range(1,max_w+1):
            if tr[i]['w']>w:
                m[(i,w)]=m[(i-1,w)]
            else:
                 m[(i,w)]=max(
                     m[(i-1,w)],
                     (m[(i-1,w-tr[i]['w'])]+tr[i]['v'])
                     )
    # 输出结果
    print(m)
    print(m[(len(tr)-1,max_w)])

if __name__ == "__main__":
    calcTreasure1()

• 递归解法

# 宝物价值和重量
tr = {(2, 3), (3, 4), (4, 8), (5, 8), (9, 10)}
# 达到最大承重
max_w = 20

# 初始化二位表格m
# key是(宝物组合，最大重量)，values是最大重量
m = {}

def thief(tr, w):
    if tr == set() or w == 0:
        m[tuple(tr), w] = 0
        return 0
    elif (tuple(tr), w) in m:
        return m[tuple(tr), w]
    else:
        vmax = 0
        for t in tr:
            if t[0] <= w:
                # 逐个从集合中去掉某个宝物，递归调用
                # 选出所有价值中的最大值
                v = thief(tr-{t}, w-t[0])+t[1]
                vmax = max(vmax, v)
        m[tuple(tr), w] = vmax
        #print("%2d ---- %2d " % (vmax,w),tr)
        return vmax

print(thief(tr, max_w))