数据结构--Dijkstra算法最清楚的讲解

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止

###基本思想

1. 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

2. 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

3. 初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

###操作步骤

1. 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

2. 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

3. 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

4. 重复步骤(2)和(3)，直到遍历完所有顶点。

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

###图解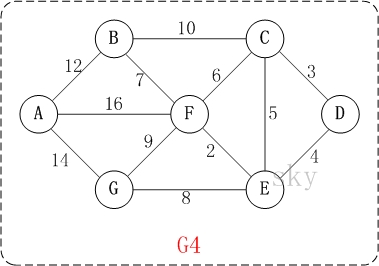

以上图G4为例，来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。以下B节点中23应为13。

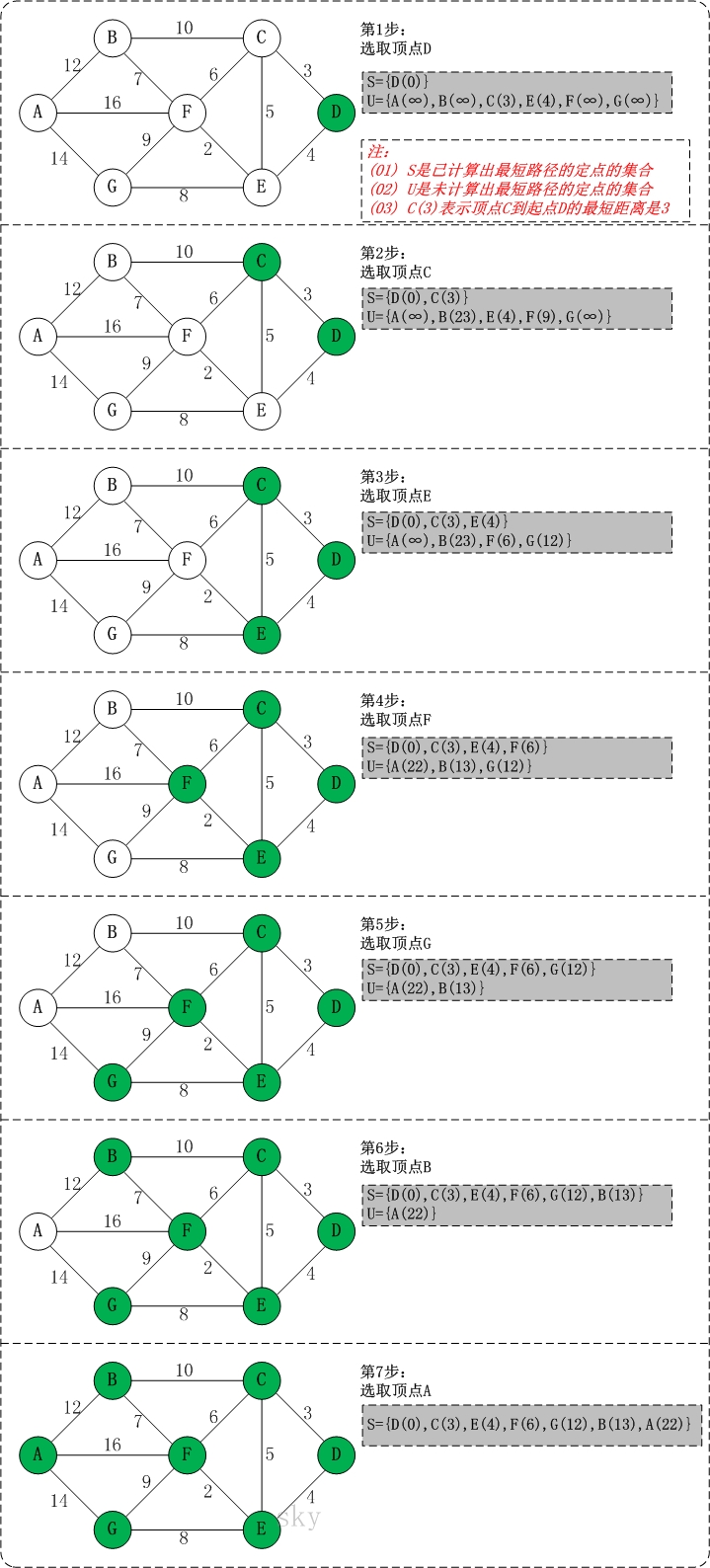
初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！

第1步：将顶点D加入到S中。
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

###代码
邻接矩阵为例，

// 邻接矩阵
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。
例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。

####Dijkstra算法

/*
 * Dijkstra最短路径。
 * 即，统计图(G)中"顶点vs"到其它各个顶点的最短路径。
 *
 * 参数说明：
 *        G -- 图
 *       vs -- 起始顶点(start vertex)。即计算"顶点vs"到其它顶点的最短路径。
 *     prev -- 前驱顶点数组。即，prev[i]的值是"顶点vs"到"顶点i"的最短路径所经历的全部顶点中，位于"顶点i"之前的那个顶点。
 *     dist -- 长度数组。即，dist[i]是"顶点vs"到"顶点i"的最短路径的长度。
 */
void dijkstra(Graph G, int vs, int prev[], int dist[])
{
    int i,j,k;
    int min;
    int tmp;
    int flag[MAX];      // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。

    // 初始化
    for (i = 0; i < G.vexnum; i++)
    {
        flag[i] = 0;              // 顶点i的最短路径还没获取到。
        prev[i] = 0;              // 顶点i的前驱顶点为0。
        dist[i] = G.matrix[vs][i];// 顶点i的最短路径为"顶点vs"到"顶点i"的权。
    }

    // 对"顶点vs"自身进行初始化
    flag[vs] = 1;
    dist[vs] = 0;

    // 遍历G.vexnum-1次；每次找出一个顶点的最短路径。
    for (i = 1; i < G.vexnum; i++)
    {
        // 寻找当前最小的路径；
        // 即，在未获取最短路径的顶点中，找到离vs最近的顶点(k)。
        min = INF;
        for (j = 0; j < G.vexnum; j++)
        {
            if (flag[j]==0 && dist[j]<min)
            {
                min = dist[j];
                k = j;
            }
        }
        // 标记"顶点k"为已经获取到最短路径
        flag[k] = 1;

        // 修正当前最短路径和前驱顶点
        // 即，当已经"顶点k的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。
        for (j = 0; j < G.vexnum; j++)
        {
            tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出
            if (flag[j] == 0 && (tmp  < dist[j]) )
            {
                dist[j] = tmp;
                prev[j] = k;
            }
        }
    }

    // 打印dijkstra最短路径的结果
    printf("dijkstra(%c): \n", G.vexs[vs]);
    for (i = 0; i < G.vexnum; i++)
        printf("  shortest(%c, %c)=%d\n", G.vexs[vs], G.vexs[i], dist[i]);
}