稀疏自动编码之反向传播算法（BP）

假设给定m个训练样本的训练集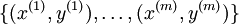，用梯度下降法训练一个神经网络，对于单个训练样本(x,y)，定义该样本的损失函数：

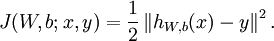
那么整个训练集的损失函数定义如下：

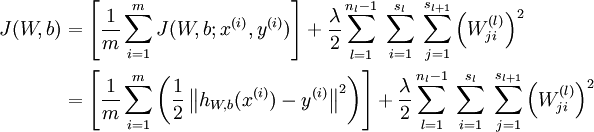
第一项是所有样本的方差的均值。第二项是一个归一化项（也叫权重衰减项），该项是为了减少权连接权重的更新速度，防止过拟合。

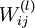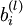我们的目标是最小化关于 W 和 b 的函数J(W,b). 为了训练神经网络，把每个参数 和初始化为很小的接近于0的随机值（例如随机值由正态分布Normal(0,ε²)采样得到，把 ε 设为0.01）, 然后运用批量梯度下降算法进行优化。由于 J(W,b) 是一个非凸函数，梯度下降很容易收敛到局部最优，但是在实践中，梯度下降往往可以取得不错的效果。最后，注意随机初始化参数的重要性，而不是全部初始化为0. 如果所有参数的初始值相等，那么所有的隐层节点会输出会全部相等，因为训练集是一样的，即输入一样，如果每个模型的参数还都一样，输出显然会相同，这样不论更新多少次参数，所有的参数还是会相等。随机初始化各个参数就是为了防止这种情况发生。

梯度下降每一次迭代用下面的方式更新参数W 和 b：

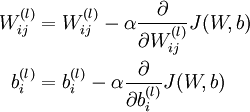
其中 α 是学习率。上述迭代的关键是计算偏导数。我们将给出一种方向传播算法，能够高效地计算这些偏导数。

由上面的总体的损失函数公式, 很容易得到偏导数公式如下：

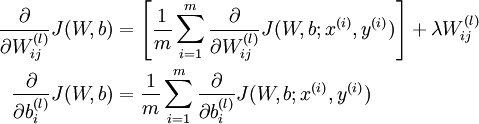
反向传播算法的思想是：给定某个训练样本(x,y)，首先进行“前向传播”计算出整个网络中所有节点的激活值，包括输出节点的输出值。那么对于 l 层的节点 i ,计算它的“残差” 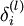 ，这个残差用来衡量该节点对输出的残差产生了多大程度的影响。对于输出节点，我们可以直接比较出网络的激活值与真正的目标值之间的残差，即 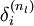（n_l  层就是输出层） 。对于隐层节点，我们用 l+1 层残差的加权平均值和 l 层的激活值来计算 .

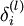下面详细给出了反向传播算法的步骤：

1. 进行前馈传播，计算每一层的中所有节点的激活值

2. 对于输出层（第n_l 层）的节点 i 的残差：

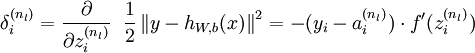
这里需要注意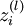： 表示第 l 层节点 i 的所有输出之和，f 是激活函数，例如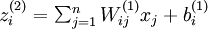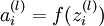，等，另外，最后一层（输出层）的假设函数的输出值就是该层节点的激活值。

3. 对于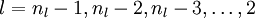 

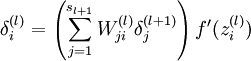
4. 计算偏导数：

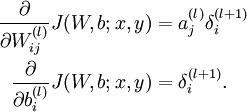
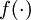下面用矩阵-向量化的操作方式重写这个算法。其中""表示matlab中的点乘。对于同样向量化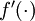， 也作同样处理，即.

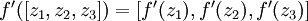BP算法重写如下：

1. 进行前馈传播，计算每一层的中所有节点的激活值

2. 对于输出层（第n_l 层）的节点 i 的残差：

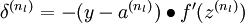
3.  对于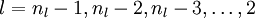 

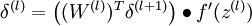
4. 计算偏导数：

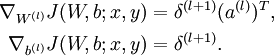
注意：在上面的第2步和第3步，，我们需要为每一个 节点 i 计算其 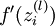 . 假设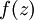是sigmoid激活函数，在前向传播的过程中已经存储了所有节点的激活值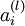，因此利用我们在

稀疏自动编码之神经网络

中推导出的sigmoid激活函数的导数求法：对于sigmoid函数f(z) = 1 / (1 + exp( − z))，它的导函数为f'(z) = f(z)(1 − f(z)).可以提前算出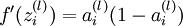，这里用到我们上面提到的.

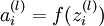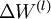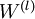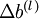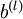最后，给出完整的梯度下降法.在下面的伪代码中，都是矩阵，，是向量。

1.  对于每一层，即所有 l , 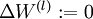,  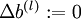(设置为全零矩阵或者向量)

2. 从第一个训练样本开始，一直到最后一个（第 m 个训练样本）：

　　a. 用反向传播计算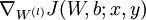 和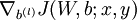

　　b. .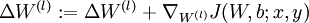

　　c. .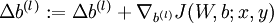

3. 更新参数：

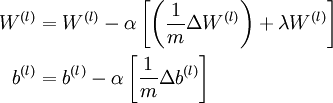
现在，我们可以重复梯度下降法的迭代步骤来减小损失函数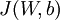 的值，进而训练出我们的神经网络。

学习来源：http://deeplearning.stanford.edu/wiki/index.php/Backpropagation_Algorithm