反正我是被坑了很久，心里增的敲难过呀！

我曾经无数次的想把它解决掉：

啊啊啊啊啊啊！

什么嘛！什么嘛！

这个空白的框框里到底要填什么嘛！！！

你已经是一个成熟的lemon了，就不能自动识别给个选项吗！！！

出于过度愤怒，某蒟蒻找了一份已经设置好了的，一看：

然后，某蒟蒻，照着格式写了一遍

然后，某蒟蒻将lemon删了

然后，某蒟蒻迫不得已又装回来了

啊！

唉...........

讲正文吧........................

看到了吗：

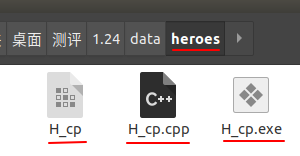
这三个文件，第一个要在 \(linux\) 下运行！第二个是cpp文件（每次spj时都编译一下）！第三个要在 \(windows\) 下运行!

所以，这个空白框框应该填：存放数据的文件夹的名字 + '/' + 对应程序的名字（填后缀要深思）：

啊！感觉整个人都舒适了不少。

lemon spj无效编译器解决方法的更多相关文章

  1. 设置height:100%无效的解决方法

    设置height:100%无效的解决方法 刚接触网页排版的新手,常出现这种情况:设置table和div的高height="100%"无效,使用CSS来设置height:" ...

  2. WPF：指定的命名连接在配置中找不到、非计划用于 EntityClient 提供程序或者无效的解决方法

    文/嶽永鹏 WPF 数据绑定中绑定到ENTITY,如果把数据文件做成一个类库,在UI文件中去应用它,可能遇到下面这种情况. 指定的命名连接在配置中找不到.非计划用于 EntityClient 提供程序 ...

  3. 移动端bug~~移动端:active伪类无效的解决方法【移动端 ：active样式无效】

    移动端:active伪类无效的解决方法[移动端 :active样式无效]2016-09-26  15:46:50 问题: 移动端开发的时候实现按钮的点击样式变化,但是在iphone[safiri Mo ...

  4. js中style.display=""无效的解决方法

    本文实例讲述了js中style.display=""无效的解决方法.分享给大家供大家参考.具体解决方法如下: 一.问题描述: 在js中我们有时想动态的控制一个div显示或隐藏或更多 ...

  5. redhat linux enterprise 5 输入ifconfig无效的解决方法

    redhat linux enterprise 5 输入ifconfig无效的解决方法   在安装完成linux后,进入终端,输入命令行ifconfig,会提示bash: ifconfig: comm ...

  6. 排错-安装SQl 2008“为SQL Server代理服务提供的凭据无效的解决方法

    安装SQl 2008“为SQL Server代理服务提供的凭据无效的解决方法 by:授客 QQ:1033553122 在Windows Server 2008安装SQL Server 2008出现的问 ...

  7. Node.js中针对中文的查找和替换无效的解决方法

    Node.js中针对中文的查找和替换无效的解决方法.   //tags的值: tag,测试,帖子 var pos1 = tags.indexOf("测"); //这里返回-1 ta ...

  8. QWidget子窗口中setStyleSheet无效，解决方法

    继承 QWidget setStyleSheet无效,解决方法. 发现 继承自QWidget的自定义类 ,使用setStyleSheet无效, 如果删除头文件中的 Q_OBJECT,setStyleS ...

  9. 表格Table宽度设置无效的解决方法

    表格Table宽度设置无效的解决方法 bootstrap中使用table时发现不管用width赋值方式都无法改变table>td的宽度 解决方法: 设置table:table-layout:fi ...

随机推荐

  1. CVE-2010-2883

    测试环境: Windows xp sp3 Adobe Reader 9.3.4 成因: CoolType.dll库的strcat函数在解析SING表中的uniqueName域时未作长度检查而造成栈溢出 ...

  2. 1092. To Buy or Not to Buy (20)-map

    给出两个字符串,判断第二个字符串中的字符是否都出现在第一个中. 是,则输出Yes,以及多余的字符的个数. 否,则输出No,以及缺失的个数. #include <iostream> #inc ...

  3. webpack简单原理及用法

    前言 如果你已经对Webpack精通了或者至少一直在工作中使用它,请关闭当前浏览器标签,无视这篇文章. 这篇文章本意是写给我自己看的,作为一篇Cookbook供快速查询和上手用.原因是虽然工作中会涉及 ...

  4. Linux第七周学习总结——可执行程序的装载

    Linux第七周学习总结--可执行程序的装载 作者:刘浩晨 [原创作品转载请注明出处] <Linux内核分析>MOOC课程http://mooc.study.163.com/course/ ...

  5. Linux命令（四）删除文件 rm

    用户可以使用 rm 命令删除不需要的文件. rm 可以删除文件或目录,并且支持通配符. 如果目录中存在其它文件则会递归删除. 删除软链接只是删除链接,对应的文件或目录不会被删除. 软链接类似于 win ...

  6. 使用fiddler的过滤条件

    使用fiddler抓包的时候经常一下子显示很多的记录,看的眼花缭乱,需要这时候需要使用过滤条件来帮助你,一般常用的有三种过滤条件: 1.域名过滤,只显示特定域名的记录: *.baidu.com表示所有 ...

  7. CF1073E Segment Sum

    数位DP,求[L,R]区间内所有"数字内包含的不同数码不超过k个的数字"之和.在状态上加一维状态压缩表示含有的数码集合.一开始读错题以为是求数字的个数.读对题之后调了一会儿. #i ...

  8. MT【164】条件化简

    (2017北大优特测试第9题) 已知实数 \(a_i\)(\(i=1,2,3,4,5\))满足 \((a_1-a_2)^2+(a_2-a_3)^2+(a_3-a_4)^2+(a_4-a_5)^2=1\ ...

  9. NOIP2018退役总结

    NOIP2018退役总结 先说下成绩,应该压线二等. 也没有什么可以抱怨的,真的是心态的问题. 在Day1的时候这么简单的一套卷子,却打了三道暴力,175本来就是省二的水平.回来以后心态就崩了,因为D ...

  10. Problem A: 踢罐子 解题报告

    Problem A: 踢罐子 Description 平面上有\(n\)个点,其中任意2点不重合,任意3点不共线. 我们等概率地选取一个点A,再在剩下的\(n-1\)个点中等概率地选取一个点B,再在剩 ...